Bazen çok basit görünen problemlerin çözümleri hiç de kolay olmuyor. İşte bir örnek:
Elimizde n adet top olsun. Bu n adet topu kaç değişik şekilde bölüştürebiliriz?
Buna görünüşte benzeyen bir soru daha önce Sarkaç’ta Ali Nesin’in Matematik ve Doğa kitabının, Sevdiğim Bir Kaç Soru bölümünden bir alıntı olarak yayınlanmıştı. Oradaki problem şu soruyu soruyordu:
Bir doğal sayıyı çeşitli biçimlerde doğal sayıların toplamı olarak yazmak istersek, kaç değişik şekilde yazabiliriz?
Örnek olarak sayımız 4 ise bunu (4), (3+1), (1+3), (2+2), (2+1+1), (1+2+1), (1+1+2) ve (1+1+1+1) gibi yazabileceğimiz için sorunun yanıtı 8 olacaktır. Aynı yazıda herhangi bir n sayısı için ise yanıtın 2 n-1 olduğu ispatlanmıştı.
Elimizdeki bölüştürme problemi benzer gibi görünse de eşdeğer değil. Sıraya önem verilmediği durumda (3+1) ile (1+3) aynı olacağından 4 top için 5 farklı bölüştürme seçeneği var: (4), (3+1), (2+2), (2+1+1) ve (1+1+1+1)
Böylelikle her n sayısı için bu sayının farklı bölünüş/parçalanışların sayısını veren p(n) fonksiyonunu elde ederiz. Bu fonksiyon da bölüşüm/parçalanış (“partition function”,) fonksiyonu ismini alır.
n sayısının küçük değerleri için p(n):
p(1)=1, p(2)=2, p(3)=3, p(4)=5, p(5)=7, p(6)=11, p(7)=15 ve p(8)=22 olarak elde edilir. Bu dizinin değerleri arasında çok da bir ilişki var gibi gözükmüyor.
Bu sayıları, küçük n için bile oturup elle hesaplamak çok kolay değil ve son derece dikkatli olmayı gerektiriyor. Algoritmik olarak da önemli sorunlar ortaya çıkarıyor. Her bölüştürme sonrası tek veya çift sayı ile karşılaştığınız zaman farklı adımlar izlemeniz gerekiyor.
Nitekim, bu fonksiyonun kapalı bir ifadesi bilinmiyor. Yani p(n)’yi herhangi bir n için sınırlı sayıda işlemle elde etmemizi sağlayacak (2n-1 gibi) bir formül henüz yok.
Kolay gözükmesine rağmen, çok zor olan bu probleme sayılar teorisi ile uğraşan matematikçilerin hepsi aşinadır.
p(n)‘i hesaplamak için yinelenen bağlantılar (recursive relations) veya asimptotik olarak (büyük n değerleri için) yaklaşılan değerler biliniyor, böylelikle teoride herhangi bir n için p(n) hesaplanabilir ama hiç de kolay olmayan algoritmalarla.
İlginç noktalar: “Sonsuzluk teorisi” filminde hayatını izlediğimiz matematikçi Ramanujan, n sayısının 4 veya 9 ile bittiği durumlarında, p(n)’in 5 ile bölünebildiğini bulmuştur.
Aslında bu sayıları hesaplamanın en kolay(!) yollarından biri Hardy-Ramanujan formülüdür. Bu kesin sonuç vermeyen bir yakınlaştırma ve büyük n değerleri için geçerli.
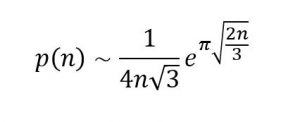 p(1019) 2012 yılında kesin olarak hesaplanmış [1]. p(n), yine büyük n değerleri için yaklaşık olarak n1/2 kadar ondalık basamaktan oluşuyor, yani p(1019)’un 3.5 milyardan fazla ondalık basamağı var.
p(1019) 2012 yılında kesin olarak hesaplanmış [1]. p(n), yine büyük n değerleri için yaklaşık olarak n1/2 kadar ondalık basamaktan oluşuyor, yani p(1019)’un 3.5 milyardan fazla ondalık basamağı var.
Ersin Yurtsever
Bilim Akademisi üyesi
Koç Üniversitesi Kimya Bölümü öğretim üyesi
[1] Johansson, F., “Efficient implementation of the Hardy–Ramanujan–Rademacher formula”, LMS Journal of Computational Mathematics, 15, 2012, p 341.
İleri Okuma: Bu konuda, Kağan Kurşungöz’ün kaleminden Matematik Dünyası‘nda yayınlanmış “Tam Sayı Parçalanışlarına Kombinatorik Bakış” başlıklı 3 yazıya ulaşmak için tıklayınız.






