Olasılık hesaplarına günlük yaşamımızda da sık sık gereksiniriz. Örneğin tavla ya da kağıt oyunları oynarken. İki kapıya üst üste birkaç gez gele atmayan tavlacı görmedim hiç. Şanssızlık deriz. Elbet, dört kez gele atan üç kez gele atandan daha şanssızdır. Bu yazının amaçlarından biri de “daha şanssız” sözcüğüne matematiksel anlam kazandırmak olacak.
Boş bir zamanınızda, evinizdeki tavlanın zarlarından birini 6000 kez atın. Gelen zarları bir kağıda yazın. Aşağı yukarı bin kez yek (1), bin kez dü (2), bin kez se (3), .. gelmeli, yani zarın her yüzünün gelme olasılığı aşağı yukarı aynı olmalı. Eğer yalnızca 500 kez penç (5) gelmişse zarınız hileli demektir. Aslında her zar hilelidir. Bir yüzü biraz daha ağır, daha eğik, daha aşınmış ya da daha kaygan olabilir. Her zarın zaafı olduğu, yakınlık duyduğu bir sayı vardır. Tavlaya oturmadan önce zarların zaafını iyi bilmek gerekir ki ona göre oynayasınız! Tavlanın da deplasmanı vardır!
Tavlamın zarlarından birini 400 kez attım. İşte elde ettiğim sonuçlar:
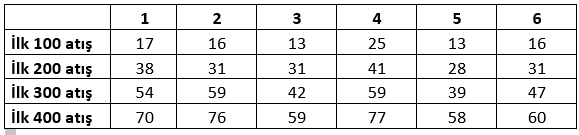
Sanki zarımın cehara (4’e) bir zaafı varmış gibi görünüyor.
Bu sonuçların ortalamalarını alalım. Örneğin 400 atışta 77 kez cehar geldiğini belirten yere $77/400$ yani $0.1925$ yazalım. Şu sonuçları buluruz:

Bunu bir grafikte gösterirsek mavi çizginin üstünde ve altında kalan değerleri görebiliriz.
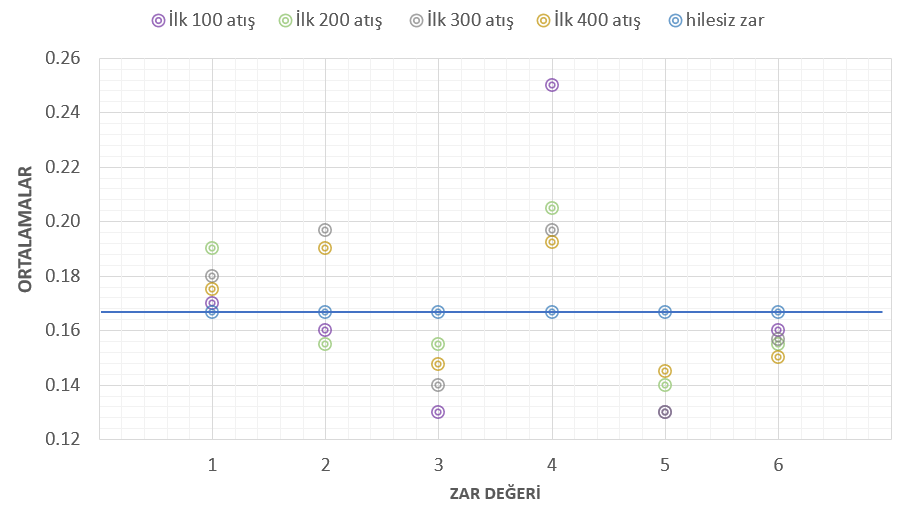
Ortalamanın kaç olması gerekiyordu?
Zarlar hilesizse ortalamanın $1/6$, yani $0.16666…$ olması gerekir (grafikteki mavi çizgi). Çünkü bir zarda 6 adet yüz vardır. Ceharların ortalaması hep yüksek çıkmış, ama bu ortalama gittikçe azalıyor ve $1/6$ ortalamasına yaklaşıyor.
6 bin kez zar attığımda, kim bilir, belki de beklenen ortalamaya daha çok yaklaşacak. Yukarıdaki sonuçlar zarımın tam zaafını göstermeyebilir. Yeterince zar atmadım. Ama sonuçların doğru olduğunu varsayarsam 400 atışta ortalama $19$ kez cehar (4), $14.5$ kez penç (5) geldiği sonucunu çıkarırım. Ona göre tavla oynamalıyım (ama önce ikinci zarla da deneyi yapmalıyım elbet!)
Hilesiz zar olduğunda
Elimize bir zar alalım. Altı yüzlü ve hilesiz bir zar. Öyle bir zarın olduğunu varsayalım. Her yüzün gelme olasılığı aynıdır:
Yek (1) gelme olasılığı, dü (2) gelme olasılığından fazla değildir Zarın altı yüzü olduğundan ve her sayının gelme olasılığına $1/6$ demek en doğrusudur. Eğer $i=1,….,6$ ise $O(i)$, $i$ sayısının gelme olasılığı olsun. Sezgilerimize dayanarak yazalım:
$$O(1)=1/6 =0.16666…$$
Tüm olasılıkların toplamının $1$ olduğuna dikkatinizi çekerim. Günlük yaşamda olasılıklar $100$ üzerine hesaplanır, ama matematikte en büyük olasılık $1$’dir. Günlük yaşamda kullanılan $\%75$in matematikçesi $0.75$ ya da $3/4$tür.
Hilesiz zarlarla çift sayı atma olasılığını bulalım, yani 2, 4, 6 sayılarından birinin gelme olasılığını. Her sayının gelme olasılığı $1/6$ olduğuna göre, çift sayı gelme olasılığı,
$$O(2)+O(4)+O(6) = \frac{1}{6} +\frac{1}{6}+\frac{1}{6}=\frac{1}{2}$$
dir. Ve elbet tek sayı gelme olasılığı da, çift sayı gelme olasılığı gibi $1/2$’dir.
Olasılık kuramcıları, yukarıdaki soruda karşımıza çıkan,
$$\{1,2,3,4,5,6\}$$
Kümesine olaylar kümesi derler. Örneğin, “yek” bir olaydır ve yek olayının (gerçekleşme olasılığı) $1/6$dır.
İki zar olduğunda
Şimdi olayları biraz zorlaştıracağız ve iki (hilesiz) zar atacağız. İlk önce iki zarı birbirinden ayıralım: Zarlardan birine birinci zar, öbürüne ikinci zar diyelim (dilerseniz zarları iki ayrı renge boyayın)
Her iki zarın da altışar yüzü olduğundan, otuz altı “olay” var:
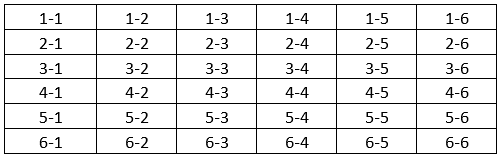
Dikkat ettiyseniz, $1-2$ ve $2-1$ olaylarını ayrı yazdım, yani iki ayrı olay olarak gösterdim. Çünkü iki zarı birbirinden ayırıyorum: Birinci zar yeki, ikinci zar düyü gösteriyorsa, gelen zara $1-2$ diyorum; tam tersiyse $2-1$. Zarlar hilesiz olduğundan her olayın olasılığı aynıdır. Dolayısıyla $O(i-j)$ sayısı, $i-j$ olayının (zarının) olasılığıysa,
$$O(i-j) = \frac{1}{36}$$
dir. Örneğin,
$$O(1-1)=O(1-2)=O(2-1)=O(3-4)$$
$$=\frac{1}{36}$$
Ama tavlada zarlar birbirinden ayırt edilmez. Biz de ayırt etmeyelim. O zaman $1-2$ ve $2-1$ olaylarını bir olay olarak algılayıp $(1,2)$ olarak gösterelim. Olayları yukarıdaki gibi sıralayalım (üstteki tabloyu ikiye katlayarak):
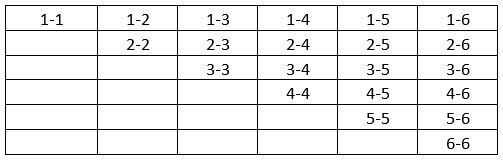
Toplam 21 olayımız var. Ama bu kez her olayın olasılığı aynı değil. Örneğin $(1,2)$ olayının olasılığı
$$\frac{1}{36}+\frac{1}{36}=\frac{2}{36}$$
Çünkü $(1,2)$ olayı için ya $1-2$ ya da $2-1$ gerekli.
$(1,2)$ olayının olasılığı şöyle bulunur:
$$O(1,2)=O(1-2)+O(2-1)=\frac{1}{36}+\frac{1}{36}=\frac{2}{36}$$
Öte yandan $(1,1)$ zarının gelme olasılığı $1/36$’dır. Demek ki, eğer $i \neq j$ ise $O(i,j)=2/36$ ve $O(i,i)=1/36$’dır. (Özellikle $2/36$ yerine $1/18$ yazmıyoruz, ilerde kolaylık olacak. )
Alıştırma olarak çeşitli olasılıklar hesaplayalım.
İki kapıya gele atma olasılığı:
Bu kapıların 1 ve 2 kapıları olduğunu varsayalım. Demek ki $(1,1)$, $(1,2)$ ya da $(2,2)$ atma olasılığını hesaplayacağız. Bu da
$$O(1,1)+O(1,2)+O(2,2)=$$
$$\frac{1}{36}+\frac{2}{36}+\frac{1}{36}=\frac{4}{36}=\frac{1}{9}$$
İki kez iki kapıya gele atma olasılığıysa
$$\frac{1}{9}\times \frac{1}{9}=\frac{1}{81}$$
Yedi kez iki kapıya gele atma olasılığıysa
$$\frac{1}{9^7}=\frac{1}{4782969}$$
Yani aşağı yukarı 5 milyonda bir.
Yek atma olasılığı:
$$O(1,1)+O(1,2)+…+O(1,6)$$
$$=\frac{1}{36}+\left(5\times \frac{2}{36}\right)=\frac{11}{36}$$
Demek ki yek atma olasılığı $1/3$’ten biraz daha az.
Cehar atma olasılığı:
Yukarıdaki gibi hesaplanır ve $11/36$ bulunur. Zar hilesizse bir sayının bir başka sayıdan farkı yoktur.
Dört hane ilerdeki bir pulu kırma olasılığı
Dört hane ilerdeki bir pulu kırma olasılığını hesaplayacağız. Dört hane ilerideki pulu kırmak için ya cehar (4) atmak gerekir ya da $(1,1)$, $(1,3)$ ve $(2,2)$ zarlarından birini (arada kapı olmadığını varsayıyoruz.)
Demek ki dört hane ilerdeki bir pulu kırma olasılığı,
$$O(4)+O(1,1)+O(1,3)+O(2,2)$$
$$=\frac{11}{36}+\frac{1}{36}+\frac{2}{36}+\frac{1}{36}=\frac{15}{36}$$
Altı ve sekiz hane ilerdeki iki puldan en az birini kırma olasılığı
Altı hane ilerdeki pulu kırmak için ya zarlardan biri 6 gelmeli ya da $(1,5)$, $(2,2)$, $(2,4)$, $(3,3)$ zarlarından birini atmalı. Sekiz hane ilerideki pulu kırmak içinse $(2,2)$, $(2,6)$, $(3,5)$, $(4,4)$ zarlarından birini atmalı. Dolayısıyla olasılık
$$O(6)+O(1,5)+O(2,2)+O(2,4)+O(3,3)$$
$$+O(3,5)+O(4,4)=\frac{11}{36}+\frac{2}{36}+\frac{1}{36}+\frac{2}{36}$$
$$+\frac{2}{36}+\frac{1}{36}+\frac{2}{36}+\frac{1}{36}=\frac{22}{36}=\frac{11}{18}**$$
Yani yüzde elliden biraz fazladır.
Ali Nesin
Bilim Akademisi üyesi
Bilgi Üniversitesi, Matematik bölümü öğretim üyesi
*Bu yazı Ali Nesin’in Matematik ve Oyun kitabındaki “Olasılık Hesapları I” başlıklı bölümden alındı.





