“Bozuk saat günde iki defa doğruyu gösterir” ifadesi dilimize İngilizceden gelmiştir. Genellikle pek çok söz söyleyen ama sözlerinin çoğu yanlış olan kişileri eleştirmek için kullanılır, çok konuşan birinin söyledikleri içerisinde bazılarının (tesadüf eseri) doğru olacağını vurgular. Açıkçası bu benzetmeyi hak edenlerin sayısı gün geçtikçe artıyor. Bilhassa medyada sık sık boy gösterip her konuda fikir beyan edenleri gördükçe bu ifade akla geliyor.
İnternet kaynakları, bu deyişin tarihinin 18. yüzyıla kadar uzadığını, 1711’deki “The Spectator” dergisinde kullanıldığını yazıyor.[1]Even a broken clock is right twice a day, Common Phrases, Erişim tarihi 10 Mart 2022. Bu ifadeyi Türkçeye çevirirken bir hata yapılmış. Orijinalinde saati tanımlamak için İngilizce “broken” kelimesi kullanılmış. Burada aslında durmuş bir saatten bahsediliyor. Durmuş bir saat devamlı olarak aynı zamanı gösterecek ve dijital olmayan yani 12 dilime ayrılmış analog bir saat kullanıyorsanız bu saatin kadranı 24 saat içinde iki defa gerçek zaman ile çakışacak.
Halbuki Türkçede “bozuk” kelimesi bozulmuş olan, görevini yapamaz duruma gelmiş olarak tanımlanıyor.[2]TDK sözlük, Erişim 10 Mart 2022. Yani zamanı ölçme işlevini yapamayan saate de bozuk diyoruz; yavaş kalan veya hızlı giden bir saat de bozuktur. Bu tanım çerçevesinde başlıktaki ifade doğru olabilir mi?
Bu deyişin doğru olmadığı hakkında pek çok yazı var, ekşi sözlük’ten gazete haberlerine kadar değişik kişiler tartışmalara katılmışlar.[3]Bozuk saat bile günde iki defa doğru zamanı gösterir demeyin sakın! Zira bu iddia kökten yanlıştır, Erişim 10 Mart 2022. Hemen hepsi ifadenin eksik olduğunu söylemekle beraber bir kısmı ise deyişin tümden yanlış olduğunu iddia ediyor.
İleri giden ya da geri kalan bir saat doğruyu hiç gösterir mi?
Bu yazıda bu ifadeyi biraz daha genelleştirmek ve normalden daha yavaş veya hızlı çalışan bozuk bir saat ne kadar sıklıkla doğruyu gösterir sorusuna bir yanıt bulmak istiyorum. Probleme biraz dikkatli bakınca çok az hızlı giden bir saatin bir gün içerisinde doğru zamanı yakalayamayacağını görebiliriz ama hiç mi yakalayamayacaktır? Bu problem düzenli bir şekilde geciken veya hızlı giden bir saat için çözülebilir.
Bir saatin göstereceği zamanı bulmak için modüler aritmetik kullanabiliriz. C.F. Gauss modüler aritmetiği 19. yüzyılda tam sayılar için tanımlamış ama tam sayıların dışında da kullanılması mümkün.
Önce doğru çalışan saate bakalım. Zaman düzenli olarak arttığı halde saatin göstergesi 12 saatlik periyotlar halinde kendini tekrar ediyor. Bu durumda problemi çözmek için $\mathrm{mod}$ fonksiyonunu kullanabiliriz. $t$ zamanında “gerçek” saatin kadranındaki ($G$) bilgiyi
$$G =t~\mathrm{mod}~ 12$$
şeklinde ifade edebiliriz. Yani $t$ sayısından 12’nin bütün katlarını çıkarınca kalanına $G$ diyoruz.
$$G= t- 12\cdot k ~~~~~~~k=0, 1,2,3….$$
Örneğin $t=14$ ise $G=14-12=2$ olacaktır. $t=27$ için ise $G=27-2\cdot 12 =3$ değerini buluruz, yani 27 saat sonra saate yeniden bakarsak ilk seferinden 3 saat farklı bir değer okuruz.
Şimdi “bozuk” saatimizin günde $d$ saat kadar hızlı gittiğini varsayalım. Bu saatin hızının normal zamanın akışına oranı
$$h=\frac{24+d}{24}$$
olur ve bozuk saatin geçtiğini iddia ettiği zaman:
$$t_B = h\cdot t$$
olur. Buradan da bozuk saatin kadranındaki değişimi bulabiliriz:
$$B = t_B~\mathrm{mod}~ 12= h \cdot t ~\mathrm{mod}~ 12$$
$G=B$ olduğunda bozuk saat gerçek saati gösterecek. Şimdi bu denklemin çözümlerine bakalım. Saatlerin periyodik davranışları nedeniyle $G=B$ denkleminin sonsuz çözümü var ve iki fonksiyonun kesiştiği noktalarda gerçek saat ve bozuk saat görüntüleri aynı olacak.
$$G=B$$
$$t ~\mathrm{mod}~ 12 \equiv t_B ~\mathrm{mod}~ 12$$
$$t- 12\cdot k_1=h\cdot t -12\cdot k_2$$
$$h\cdot t- t =t(h-1)=12\cdot (k_2-k_1) $$
ya da
$$t=\frac{12\cdot k}{h-1}$$
olarak buluruz. $k$ bir tam sayıdır. Bu formüle $k=1$ için $h$ değerinin $d$ cinsinden tanımını koyarsak
$$t=\frac{288}{d}$$
buluruz. Yani bozuk bir saat günde $d$ saat kadar hızlı gidiyorsa $t=288/d$ kadar zaman sonra ilk defa doğru zamanı gösterecek. Eğer saat günde $d$ kadar geri kalıyorsa, simetri nedeniyle (doğru ve bozuk saatlerin yerleri değiştirilebilir) çözüm aynı olmak zorunda.
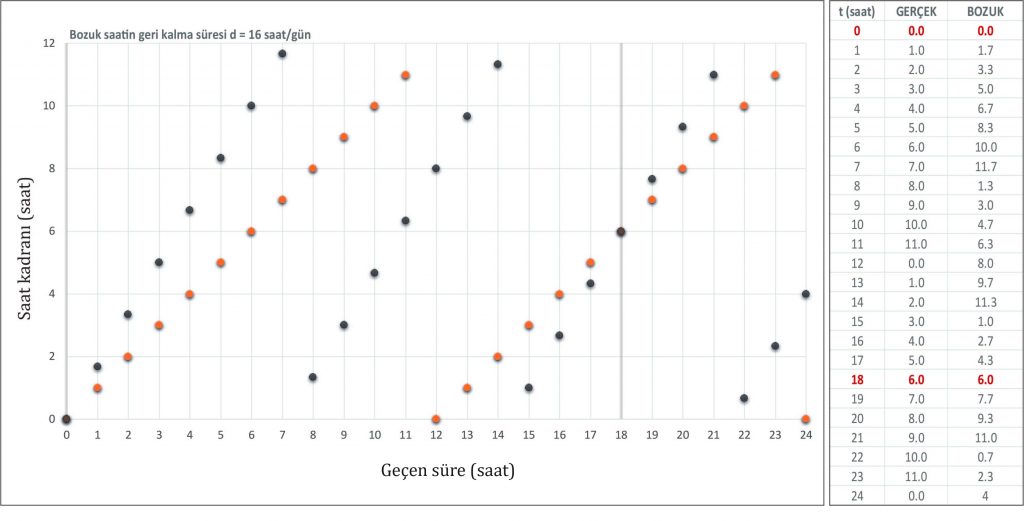
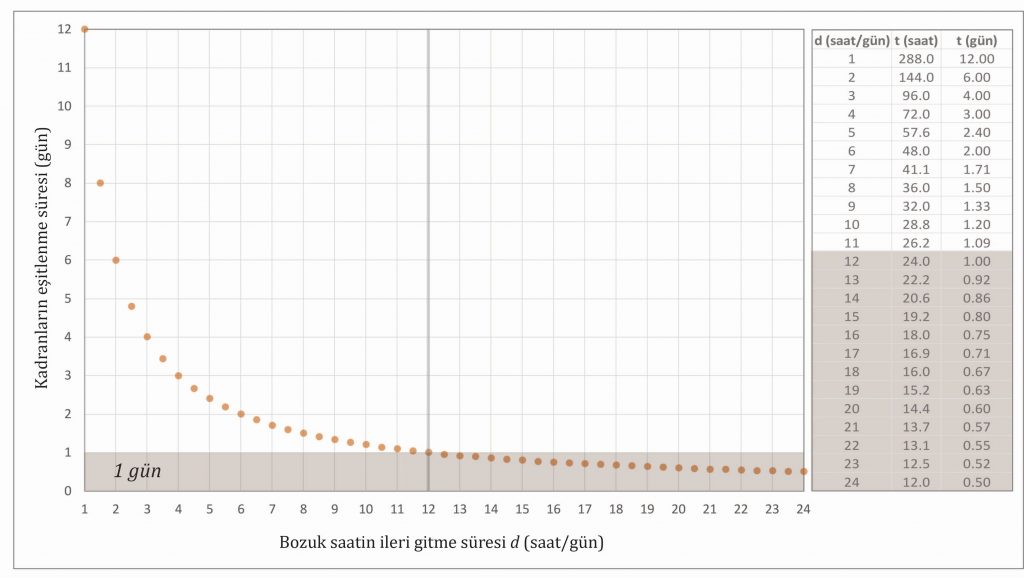
Sonuç olarak bozuk saatler de bazen doğruyu gösterir; günde 12 saatten fazla geri kalan veya ileri giden bir saat ise ilk gün içerisinde bir kez doğruyu gösterecektir.
Ersin Yurtsever
Bilim Akademisi üyesi, Koç Üniversitesi Kimya Bölümü
Modüler aritmetik konusundaki yardımları için Koç Üniversitesi, Elektrik-Elektronik Bölümü’nden Alper Erdoğan’a teşekkür ederim.
 Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Notlar/Kaynaklar
| ↑1 | Even a broken clock is right twice a day, Common Phrases, Erişim tarihi 10 Mart 2022. |
|---|---|
| ↑2 | TDK sözlük, Erişim 10 Mart 2022. |
| ↑3 | Bozuk saat bile günde iki defa doğru zamanı gösterir demeyin sakın! Zira bu iddia kökten yanlıştır, Erişim 10 Mart 2022. |






