Antik Yunan halkı keşke origami bilseydi…
Eukleides (Öklid) ünlü Elemanlar[1]Sertöz S. (2021) “Öklid’in Elemanları”, TÜBİTAK. kitabında geometrik yapıları işaretsiz cetvel ve pergel ile inşa eder. Antik Yunan geometricileri bu geleneği sürdürür ve her şeyi cetvel ve pergel ile çizmeye çalışır, ancak günlük hayatta kullandığımız cetvel ve pergel ile değil, idealize edilmiş işaretsiz cetvel ve pergel ile. İdealize edilmiş cetvelin üzerinde herhangi bir uzunluk birimi işaretlenmemiştir, sadece iki noktayı birleştiren doğru çizmek ve var olan bir doğruyu uzatmak için kullanılır. İdealize edilmiş pergel ise gerçek pergelin aksine keyfi olarak açılabilir ve yine üzerinde herhangi bir işaret yoktur. Sadece önceden inşa etmiş olduğunuz uzunluk genişliğinde açılabilir ve o uzunluğa eşit yarıçapta bir çember çizilebilir.
Antik Yunan geometricilerin sadece işaretsiz cetvel ve pergel kullanarak çözmeye çalıştığı üç klasik geometri problemi vardır:
-
-
- Bir açıyı üçe bölme,
- Verilen bir küpün hacminin iki katı hacimde bir küp çizme,
- Verilen bir dairenin alanı ile aynı alana sahip bir kare çizme.
-
1837 yılında Fransız matematikçi Wantzel, bir açıyı üçe bölme ve bir küpün hacmini iki katına çıkarma problemlerinin sadece işaretsiz cetvel ve pergel kullanarak çözülmesinin imkânsız olduğunu kanıtladı. Çünkü bu problemlerin üçüncü dereceden bir denklemin köklerini bulma problemine eşdeğer olduğunu gösterdi.[2]Wantzel, P. (1837) “Recherches sur les moyens dereconnaître si un probleme de Géométrie peut serésoudre avec la regle et le compas”, Journal de mathématiques pures et appliquées, série 1(2), 366-372. Oysa origami geometrisi ile ilk iki problemi çözmek mümkün. Şimdi bu çözümleri inceleyelim.
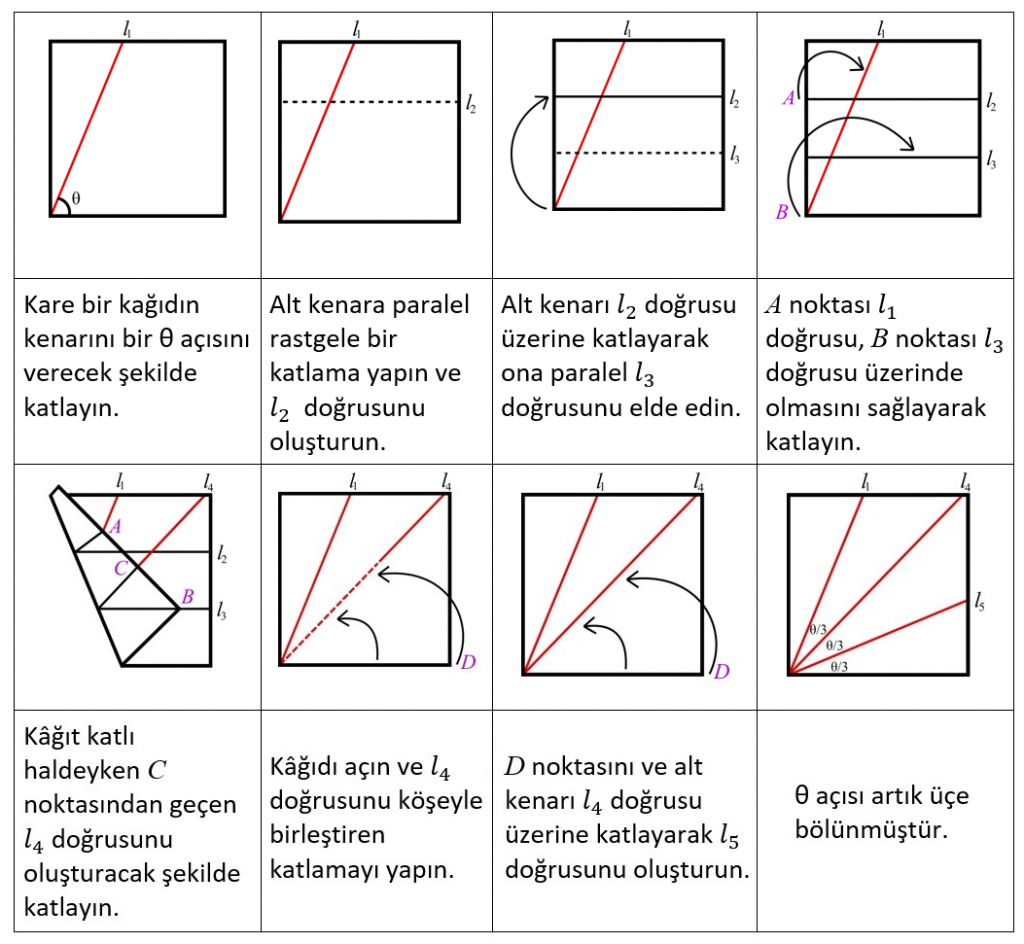
Origami ile bir açıyı üçe bölme
Bu katlama metodu 90 dereceden küçük açılar için işe yarıyor. Metodu ilk Hisashi Abe 1980’de bulmuş. 90 dereceden büyük açılar için de çalışan bir yöntem var, bir kâğıtla bu metodu bulmak için denemeler yapabilirsiniz.
Küpün hacmini iki katına çıkarma
İkinci problem olan bir küpü iki katına çıkarma probleminin çözümsüz olması antik Yunan halkı için trajik sonuçlanmıştı. Efsaneye göre yıkıcı bir veba salgını ile karşı karşıya kalan antik Yunan Delos adası halkı Delfi şehrinde bir kâhinin yanına gider. Kâhin, Delos halkına küp şeklindeki sunaklarının hacminin iki katına sahip yeni bir sunak yaptıklarında veba salgınının sona ereceğini söyler. Antik Yunan halkı soruyu yanlış anlar ve eski sunağın kenarını iki katına çıkararak yeni bir sunak yapar. Fakat bu durum tanrıları memnun etmez çünkü bu durumda sunağın hacmi iki katı yerine sekiz katına çıkmıştır.[3]Zhmud L. (2008) The origin of the history of science in classical antiquity, Peripatoi, sayı 19, sayfa 84.
Antik Yunan halkı keşke origami bilseydi, nihayetinde veba salgını kolayca sona erebilirdi. Şaka bir yana bu problemi çözmek için neye ihtiyacımız var?
Kenarı $a$ ve hacmi $V=a^3$ olan bir küp alalım. $b^3 = 2 V$ olan yeni bir küp oluşturmak istiyoruz.
$$b^3 = 2 V = 2 a^3$$
$$b= \sqrt[3]{2} a$$
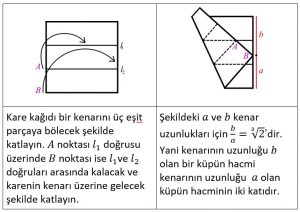
Bu durumda $\sqrt[3]{2}$ sayısını elde etmeliyiz ki kenarları ne kadar büyüteceğimizi bilelim. Wantzel sayesinde işaretsiz cetvel ve pergel kullanarak $\sqrt[3]{2}$ elde etmenin imkânsız olduğunu biliyoruz. Ancak, origami geometrisi ile $\sqrt[3]{2}$ sayısını elde etmek mümkün. Şimdi de Peter Messer’in 1986’da bulduğu inşa metodunu yakından inceleyelim.
Origami ile bir küpün hacmini iki katına çıkarma:
Dairenin alanına eşit bir kare çizme
Peki, üçüncü problem alanı bir dairenin alanına eşit olan bir kare çizme problemini origami ile çözebilir miyiz?
Yarıçapı $r$ olan bir dairenin alanı $\pi r^2$ ve kenarları $a$ olan bir karenin alanı $a^2$ dir. İkisinin alanlarının eşit olması için
$$a^2 = \pi r^2~~~~\text{yani} ~~~~~ a=\sqrt{\pi} r$$
olmalı.
Çözüm için aşkın (transandantal) bir sayı olan $\sqrt{\pi} $ sayısını işaretsiz cetvel ve pergel kullanarak elde etmek gerekir. Katsayıları rasyonel olan bir polinomun kökü olmayan sayılara aşkın sayı denir, $\pi$ sayısının aşkınlığını 1882 yılında Lindemann göstermişti.[4]Lindemann, F. (1982) “Über die Zahl $\pi$”, Mathematische Annalen, 20, 213–225. Lindemann’ın çalışması alanı bir dairenin alanına eşit olan bir kare çizme probleminin işaretsiz cetvel ve pergel kullanarak çözülemeyeceğini ispatlar. Origami ile $\pi$ sayısına yakın sayıların elde edildiği katlama metotları biliniyor. Örneğin 22/7 sayısını katlayabiliriz. Şu an için bırakın $\sqrt{\pi} $ sayısını, $\pi$ sayısının katlandığı bir metot bilinmiyor. Katlanıp katlanamayacağını söylemek bile ciddi bir ispat yapmayı gerektiriyor.
Kolay gelsin, iyi eğlenceler!
Sinem Onaran
Hacettepe Üniversitesi Matematik Bölümü, BAGEP 2020
Origamiyle geometri egzersizleri [5]Sundara Rao, T. (1893) “Geometric exercises in paper folding”, Addison & co.
 Bu eser görseller dahil Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Bu eser görseller dahil Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Notlar/Kaynaklar
| ↑1 | Sertöz S. (2021) “Öklid’in Elemanları”, TÜBİTAK. |
|---|---|
| ↑2 | Wantzel, P. (1837) “Recherches sur les moyens dereconnaître si un probleme de Géométrie peut serésoudre avec la regle et le compas”, Journal de mathématiques pures et appliquées, série 1(2), 366-372. |
| ↑3 | Zhmud L. (2008) The origin of the history of science in classical antiquity, Peripatoi, sayı 19, sayfa 84. |
| ↑4 | Lindemann, F. (1982) “Über die Zahl $\pi$”, Mathematische Annalen, 20, 213–225. |
| ↑5 | Sundara Rao, T. (1893) “Geometric exercises in paper folding”, Addison & co. |