“Gerçekten evrenin sırrını arıyorsanız, benim yaptığım gibi sayılara gelin. Sonsuzluk her şeyin cevabıdır. Sayı sonsuzdur.” – Cahit Arf
Eğer siz de Cahit Arf’a katılıyorsanız evrenin sırrını aramak gibi zorlu bir serüvende uğramanızda fayda olabilecek bir matematiksel örüntüler diyarı olabilir. Bahsettiğimiz diyar yüzbinlerce tam sayı örüntüsü barındıran bir veritabanı: OEIS.
Temelleri 1964’te matematikçi Neil Sloane tarafından atılan OEIS (On-Line Encyclopedia of Integer Sequences – Tam sayı dizilerinin çevrimiçi ansiklopedisi) günümüzde çevrimiçi hizmet veren arayüzü ile yaklaşık 350000 tam sayı dizisine ev sahipliği yapıyor.[1]Sloane, N. (2021). The OEIS: A Fingerprint File for Mathematics, https://arxiv.org/abs/2105.05111 Çok farklı uzmanlık alanlarına ait bu diziler ile ilgili referanslar, hesaplama betikleri, formüller gibi birçok bileşeni de bir arada sunan OEIS gerçek bir ansiklopedi niteliğinde. Tek yapmanız gereken ise aradığınız dizinin ilk birkaç terimini sorgulatmanız. Arayüz size ilgili tüm dizilerin bilgilerini anında listeliyor.
Bir wiki sayfası olarak yapılandırılmış OEIS özgün tüm katkılara açık ve geliştirilmeye elverişli bir yapıda, bir öneride bulunmak için ise sadece kayıt olmak ve prosedürleri takip etmek yeterli. Diğer yandan tek bir örnek için dahi birçok bileşen varken yüzbinlerce dizinin ve yeni eklenecek olanların yaşam döngüsünü yönetmek ciddi bir efor, uzmanlık ve takım çalışması gerektiriyor.
Tamamen gönüllü editörlerin titizlikle ele aldığı süreçler ile büyüyen ve herkese açık olan bu matematiksel veritabanı sunduğu çeşitliliği kullanım kolaylığı ile birleştirdiğinden araştırmacılar için alternatifsiz bir kaynak.[2]Sloane, N. (2018). The On-Line Encyclopedia of Integer Sequences, Notices, Amer. Math. Soc., 65, 1062-1074.
Birçok araştırmacı keşiflerini OEIS’in sunmuş olduğu koleksiyona ve bu koleksiyonda beklenmedik şekilde karşılarına çıkan bir dizi ile fark ettikleri bir bağlantıya borçlu olduğunu belirtiyor. OEIS’e atıf yapan yayınların sayısı da her yıl kayda değer şekilde artıyor ve 7 Eylül 2021 itibariyle 9500’ün üzerinde makalede OEIS’e atıf var.[3]Works citing OEIS, https://oeis.org/wiki/Works_Citing_OEIS, Erişim 22.09.2021
OEIS’ten bir örnek
İlginç bir problem özelinde örnek vermemiz faydalı olabilir. Bir düzgün çokgenin tüm köşegenlerinin meydana getirdiği bölgeleri ve iç kesişim noktalarının sayısını incelemek istediğimizi düşünelim. Soru bir kare, beşgen, altıgen ve hatta yedigen için çok zorlanmadan çözebileceğimiz seviyede görünüyor aşağıdaki şekilde.[4]Gonzalez, J. https://oeis.org/A006561/a006561_1.png
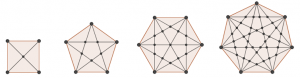
Gözlemlerimizi yazılı hale getirdiğimizde sırasıyla iç kesişim noktaları için 1, 5, 13, 35 ve bölgeler için ise 4, 11, 24, 50 sayılarını elde ettiğimizi görürüz. Çokgenlerin kenar sayıları arttıkça problemin hayal gücümüzün sınırlarını zorlayacak hale geleceği şüphesiz. Eğer bu iki bulgumuzu OEIS veritabanında sorgularsak karşımıza ilk sırada çıkan diziler A006561 ve A007678 olduğunu görürüz ki buradan incelemek istediğimiz probleme[6]Poonen B. ve Rubinstein M. (1998). The number of intersection points made by the diagonals of a regular polygon, SIAM J. Discr. Math., 11:1, 135–156. ve literatürde bu problemle ilgili yapılan yayınlara ulaşmış oluruz. Böylece yine aynı problem için kenar sayıları büyüdükçe olacakları da gözlemleme şansımız olur ve matematiksel bir örüntünün renklerle betimlenmesine şahitlik etmiş oluruz.[7]Blomberg, L., Shannon, S.R. ve Sloane, N. J. A. (2021) Graphical Enumeration and Stained Glass Windows, 1: Rectangular Grids, INTEGERS dergisine preprint, yeni versiyon May 21 2021
Yukarıdaki örnekte olduğu gibi yapısallaştırılmış veriden bilgisayarların gücü ile bilimsel değer yaratmaya da ilginç bir örnek olarak görülebilir OEIS. Kim bilir, belki gelecekte OEIS veritabanının sahip olduğu bu veri setleri araştırmacılar olmadan da yapay öğrenme ile otomatize keşifler yapılmasına vesile olur.[10]Wu, C. (2018). Can machine learning identify interesting mathematics? An exploration using empirically observed laws. ArXiv, abs/1805.07431.
Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Notlar/Kaynaklar
| ↑1 | Sloane, N. (2021). The OEIS: A Fingerprint File for Mathematics, https://arxiv.org/abs/2105.05111 |
|---|---|
| ↑2 | Sloane, N. (2018). The On-Line Encyclopedia of Integer Sequences, Notices, Amer. Math. Soc., 65, 1062-1074. |
| ↑3 | Works citing OEIS, https://oeis.org/wiki/Works_Citing_OEIS, Erişim 22.09.2021 |
| ↑4, ↑5 | Gonzalez, J. https://oeis.org/A006561/a006561_1.png |
| ↑6 | Poonen B. ve Rubinstein M. (1998). The number of intersection points made by the diagonals of a regular polygon, SIAM J. Discr. Math., 11:1, 135–156. |
| ↑7, ↑8, ↑9 | Blomberg, L., Shannon, S.R. ve Sloane, N. J. A. (2021) Graphical Enumeration and Stained Glass Windows, 1: Rectangular Grids, INTEGERS dergisine preprint, yeni versiyon May 21 2021 |
| ↑10 | Wu, C. (2018). Can machine learning identify interesting mathematics? An exploration using empirically observed laws. ArXiv, abs/1805.07431. |
