Benford kanununun ilk ortaya çıkışı matematikçi ve astronom Simon Newcomb’a (1835-1909) atfedilir. Newcomb, hesap makineleri yokken sıklıkla kullanılan logaritma tablosu kitaplarında, ilk basamağı küçük rakamlara denk düşen sayfaların, ilk basamağı büyük rakamlara denk düşen sayfalara göre daha fazla yıprandığını gözlemlemişti.
Newcomb, 1881’de bu gözlemini matematiksel olarak formülize eden bir makale yazdı.[1]Newcomb, S. (1881) Note on the frequency of use of the different digits in natural numbers, American Journal of Mathematics, Vol. 4, No.1, pp. 39-40. Newcomb’un ardından şimdilerde Benford kanunu olarak bildiğimiz konu, popülerleşme anlamında iki kez sıçrama yaşadı. Bunlardan ilki kanuna ismini veren Benford’un çalışmaları sonucu oldu, ikincisiyse Mark Nigrini’nin bu kanunun gerçek dünyadan güzel bir uygulamasını ortaya koymasıyla gerçekleşti.
Frank Benford, 1883 ile 1948 yılları arasında yaşamış bir fizikçi ve elektrik mühendisidir. Kendisi, dışarıdan birbirleriyle alakasız gibi görünen çeşitli veri kümeleri üzerinde, burada tartışacağımız üzere oldukça ilginç bir motifi tespit etti.[2]Benford, F. (1938). The Law of Anomalous Numbers. Proceedings of the American Philosophical Society, 78(4), 551–572. Bu motifin ne olduğuna geçmeden birkaç tane şemaya bakalım.
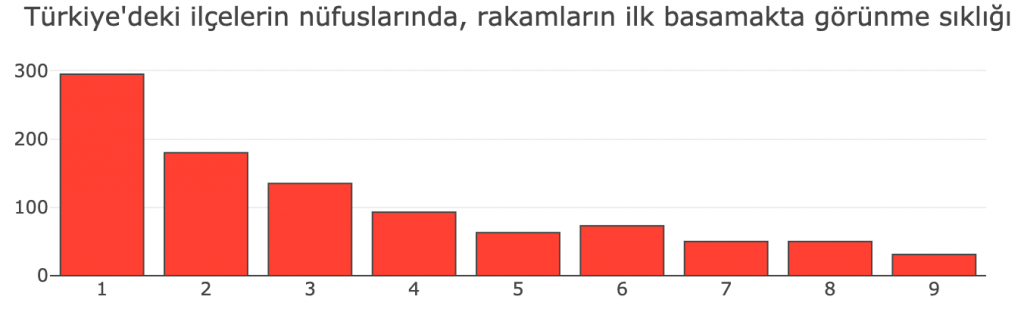
İlkinde Türkiye’deki 970 ilçenin nüfuslarına bakıyoruz. Aşağıdaki şemamız bu veri kümesindeki sayıların ilk basamaklarına bakıyor ve ilk basamaktaki rakamlara göre sıklıkları gösteriyor. Örneğin, 970 ilçemizden yaklaşık 300 tanesinin nüfusunun ilk rakamı 1’miş.[3]Bu veri kümesini Benford kanunu üzerine düşünürken 2018 yılında bulmuştum. O zaman internette bulduğum bu verinin bulunduğu siteye şu an ulaşamıyorum.
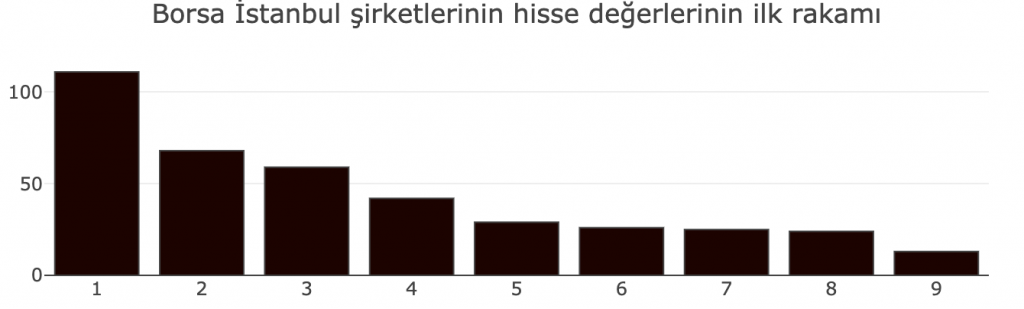
Bir sonraki verimiz İstanbul Borsasında işlem görmekte olan 397 şirketin hisse fiyatlarının ilk basamaklarındaki rakamların sıklığı.[4]Veri, İş Yatırım’ın sitesinden alınmıştır. https://www.isyatirim.com.tr/tr-tr/analiz/hisse/Sayfalar/default.aspx, Erişim: 09/01/2021
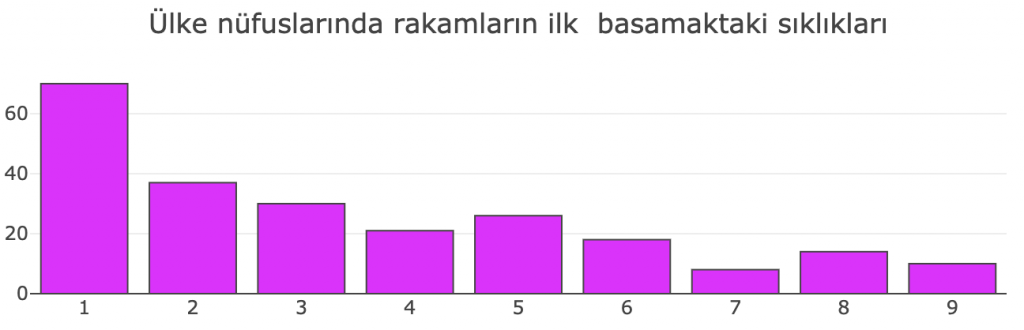
Sıradaki veride de 235 ülkenin nüfuslarının ilk basamaklarındaki rakamların sıklıklarını görüyoruz.[5]Veri, Worldometer internet sitesinden alınmıştır, https://www.worldometers.info/, Erişim: 9 Ocak 2021
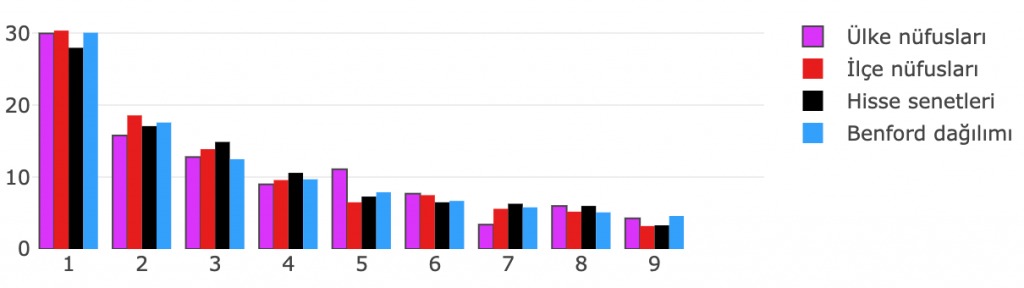
Bu verilerde ortak olarak gördüğümüz nokta, 1’den 9’a doğru gidildikçe o rakamla başlayan sayıların sıklığının üç aşağı beş yukarı benzer şekilde düşmesi.
Belki de önemli bir diğer nokta olarak 1’den 9’a kadar olan sayıları rastgele seçseydik oluşmasını bekleyeceğimiz durumdan oldukça uzak olduğumuzu da söylememiz gerekli.
Bu üç örneğimizde gördüğümüz ortak motif daha pek çok yerde ortaya çıkıyor. Benford bu ortak davranışı fark ettiğinde bu tarz durumları modelleyebilmek için ortaya bir olasılık dağılımı attı:
Buradaki olasılıklar aslında matematiksel bir formülden geliyor. Bu, Benford’un bizlere sunduğu, 1‘den 9‘a kadar olan bir a doğal sayısına
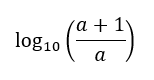
olasılığı atayan bir olasılık dağılımı. Formülün çıkarılışının elbette ki bir altyapısı var ama burada teknik detaylara hiç girmiyoruz.
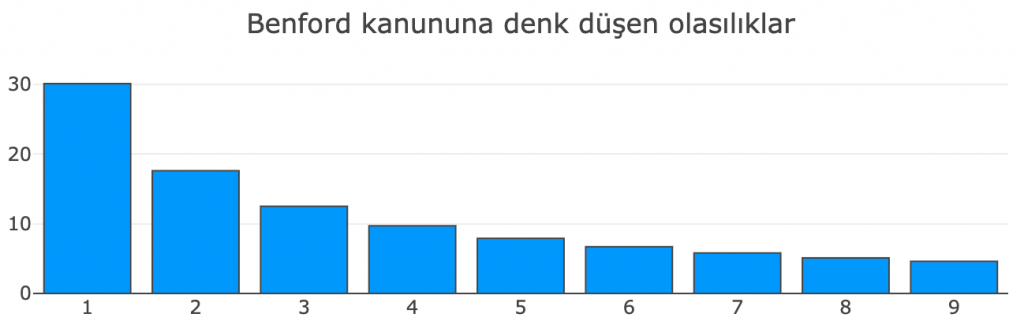
Aşağıdaki şemada da Benford dağılımına denk düşen olasılıkları görüyoruz. Bu oranlar bir olasılık modelinden geldiğinden “teorik değerler” olarak adlandırabilir ve pratikte karşılaştığımız durumlarla kıyaslanabilir.
Peki burada karşımıza çıkan olgunun altında yatan sebep ne? İş biraz karışık ve üzerine kitaplar dahi var. Ancak birçok durumu netleştirebilecek basit bir açıklama verebiliriz. Bankada 100 liranız var, aylık faiz % 20 olsun. O halde paranızın 100 liralardan 200 liralara geçmesi, bir başka deyişle, 1 rakamı ile başlayan bir sayıdan 2 rakamı ile başlayan bir sayıya geçmesi dört ay sürer:
- 100 TL – 120 TL – 144 TL – 172,8 TL – 207,36 TL (Paramızın ilk basamağı dört ayda değişti)
Peki ya bankada ilk başta 200, 300, 400 veya 500 liramız olsa paramızın büyümesi nasıl olurdu?
- 200 TL – 240 TL – 288,8 TL – 345,6 TL (Paramızın ilk basamağı üç ayda değişti)
- 300 TL – 360 TL – 432 TL (Paramızın ilk basamağı iki ayda değişti)
- 400 TL – 480 TL – 576 TL (Paramızın ilk basamağı iki ayda değişti)
- 500 TL – 600 TL (Paramızın ilk basamağı bir ayda değişti)
- …
Gördüğünüz üzere, 200, 300, 400 ve 500 TL ile başladığımızla, ilk bakiyemiz 100 TL olan durumdan daha çabuk rakam değişikliği yaşadık ilk basamakta. Hatta ilk rakamımız 5 ya da daha fazlaysa rakamımızın değişmesi sadece bir ay sürdü.
Yani, üssel olarak büyüyen[6]Alpar, A. (2020) Üssel artış nedir? https://sarkac.org/2020/03/ussel-artis-nedir/ verileriniz varsa (örneğin, şehirlerin nüfusu, bankalardaki paralar, vs.) Benford kanunu ile karşılaşmak oldukça doğal.
Sahteciliklerin tespiti
Yukarıda bahsettiklerimiz başlı başına ilginç olmasına karşın Benford kanunu, Mark Nigrini’nin bulduğu bir uygulama sahası ile iyice aktif hale geldi. Buradaki konu vergi ve muhasebeciliğe dair yapılabilecek olası sahtekârlıkların tespiti üzerine. Basit bir şekilde anlatmak gerekirse, ABD’de West Virginia Üniversitesi Muhasebe Bölümü öğretim üyesi Nigrini bu iki sahadaki çeşitli bildirimlerin Benford kanununa uyması gerektiğini gözlemlemiş, sonrasında şu şekilde bu gözleminin usulsüzlüklerin tespit edilmesinde kullanılabileceğini fark etmiştir:
Eğer bir kişi rakamları rastgele değiştirirse, her bir rakamı aşağı yukarı 1/9 olasılıkla seçecektir ve bu da, olması gerekenden istatistiksel olarak tespit edilebilir sapmalar oluşturacaktır.
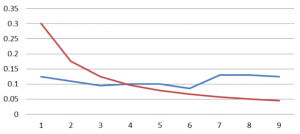
Örneğin aşağıdaki şeklimizde kırmızı çizgi Benford kanununa denk düşerken, mavi çizgi, sayılarımız bilgisayar tarafından rastgele seçildiğinde, ilk basamakta rakamlarımızın oluşma sıklığını gösteriyor – detaylara girmiyorum ama sayıların bilgisayar tarafından belirli bir aralıktan rastgele seçildiğini, sonrasında da ilk basamağına bakıldığını düşünelim. Daha önce de belirttiğimiz üzere, bu, istatistiksel testler aracılığıyla fark edilebilir bir durum yaratıyor.
Tabii ki sadece bu veriye dayalı bir istatistiksel test üzerinden sonuca varmak zor. Aslında dolandırıcılarla denetçiler arasındaki durumu bir nevi stratejik savaşa benzetebiliriz. Dolandırıcılar, denetçilerin kullandıkları teknikleri anlamaya çalışarak veri kümesi üzerinde ona göre oynamak isterken, denetçiler ise dolandırıcıların yeni oluşturabilecekleri stratejileri tahmin edip, onları da yakalayabilmek için çalışırlar.
Örneğin birinci basamak fenomenini öğrenen bir dolandırıcı bu sefer ikinci ya da sonraki basamaklarda da oynamalar yapmaya başlayabilir ve tarihsel olarak gerçekleştiği üzere, sonrasında denetçiler de ikinci basamak ya da sonraki basamaklar için de Benford kanunu türevlerinin geçerli olduğunu gözlemleyebilirler.
Bunu daha da karıştırabiliriz. Diğer basamakları düşünebilir, tüm basamakları düşünüp bunların üzerine çeşitli ağırlıklar koyabilir ya da tamamen alternatif istatistiksel testler hazırlayabiliriz. Bunlar ve daha fazlası için okurlara başlangıç seviyesinde şu kitabı tavsiye ederim: Nigrini, Mark J., Benford’s Law: Applications for forensic accounting, auditing, and fraud detection, John Wiley & Sons, 2012.
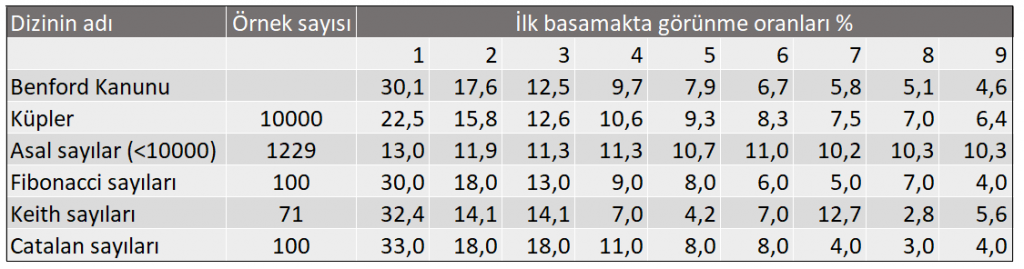
Son olarak Benford kanununun matematikteki birçok sayı dizisinde de ortaya çıktığını not düşelim. Aşağıdaki tabloda çeşitli sayı dizileri için ilk basamakta oluşan rakamların sıklıkları veriliyor.
Bir örnek olarak Fibonacci sayılarına baktığımızda buradaki ilk basamakların Benford modeline oldukça yakın olduklarını görüyoruz. Matematikle içli dışlı olmayan biri için bu şaşırtıcı olabilir ama matematik bölümünde ilk sene öğrendiğimiz şeylerden bir tanesi, Fibonacci sayılarının üssel olarak büyüdüğüdür. Hatırlarsanız üssel büyüme olan durumlarda Benford dağılımını gözlemek oldukça doğaldır.
Burada Benford dağılımının nerelerde ortaya çıkabileceğine dair ufak bir giriş yaptık, ancak konu oldukça geniş. Örneğin, nerede çıkmayacağını sorgulamak da oldukça faydalı bir zihinsel süreç.
Covid-19 verileri ve Benford Kanunu
Bugünlerde gündemimiz Covid-19. Bir yandan tıp insanlarına, bizlerin hayatlarını kurtarmak gibi büyük bir iş düşerken bir yandan da istatistikle ilgilenen birçok bilim insanı duruma farklı açılardan yaklaşarak katkıda bulunmaya çalışıyor. Bunların başında salgının yayılmasını modellemek gelse de işin bir de başka boyutu var. Dünyanın hemen her ülkesinde resmi kurumlara karşı bir güvensizlik mevcut ve gündelik vaka, ölüm sayıları gibi birçok veri kümeleri inceleme altında. Amaç gerçek sayıların üzerinde oynama yapılıp yapılmadığını anlamak. Bu yazıdaki bahsettiğimiz vergi bildirimleri ve muhasebecilikteki sahtekarlıkların Benford kanunu ile yakalanması durumunun, yaşamakta olduğumuz süreçte işe yarayıp yaramayacağını da düşünmek üzere sizlere bırakalım.
Ümit Işlak
Boğaziçi Üniversitesi Matematik Bölümü
 Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. Görseller Wikimedia Commons’dan temin edilmiştir. İçerik kullanım koşulları için tıklayınız.
Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. Görseller Wikimedia Commons’dan temin edilmiştir. İçerik kullanım koşulları için tıklayınız.
Notlar/Kaynaklar
| ↑1 | Newcomb, S. (1881) Note on the frequency of use of the different digits in natural numbers, American Journal of Mathematics, Vol. 4, No.1, pp. 39-40. |
|---|---|
| ↑2 | Benford, F. (1938). The Law of Anomalous Numbers. Proceedings of the American Philosophical Society, 78(4), 551–572. |
| ↑3 | Bu veri kümesini Benford kanunu üzerine düşünürken 2018 yılında bulmuştum. O zaman internette bulduğum bu verinin bulunduğu siteye şu an ulaşamıyorum. |
| ↑4 | Veri, İş Yatırım’ın sitesinden alınmıştır. https://www.isyatirim.com.tr/tr-tr/analiz/hisse/Sayfalar/default.aspx, Erişim: 09/01/2021 |
| ↑5 | Veri, Worldometer internet sitesinden alınmıştır, https://www.worldometers.info/, Erişim: 9 Ocak 2021 |
| ↑6 | Alpar, A. (2020) Üssel artış nedir? https://sarkac.org/2020/03/ussel-artis-nedir/ |