19. yüzyıl sonunda fizik bilimi büyük başarılar kazanmıştı. Maxwell denklemleriyle elektrik, mıknatıslık ve ışığın aslında elektromanyetik alanlar ve dalgaların farklı yüzleri olduğu anlaşılmıştı. Işık elektromanyetik dalgalar arasında bizim gözümüzün algıladığı çeşidiydi. Kısa süre içinde radyo, mor-ötesi (ultraviyole), kızıl-altı (infrared), X-ışını gibi hepsi aynı yasalara uyan aynı ışık hızı c ile yayılan elektromanyetik dalga çeşitleri bulundu. Öte yandan termodinamik ve istatistik fiziğin gelişmesiyle ısı da hesaba katılarak enerjinin bütün biçimlerini içeren enerji korunumu merkezi bir kavram olarak yerleşmişti. Bu büyük başarılarla birlikte klasik fizik tamamlanmış gibi görünecekken, çok temel birtakım gözlemlerin klasik fizikle çeliştiği, hiçbir şekilde anlaşılmadığı, tutarsızlıklara yol açtığı ortaya çıktı. Böylece bilim büyük bir zaferden büyük bir krize yönelmişti.
20. yüzyılın başlarında bu krizin bir yönü Einstein’ın görelilik teorisiyle, bir çok problemi içeren başka bir yönü de kuantum mekaniğiyle aşıldı. Kuantum teorisine göre nesneler hem parçacık hem dalga özellikleri taşırlar. Bir parçacık aynı zamanda bir dalgadır. Parçacık özellikleri enerji ve momentum ile dalga özellikleri frekans ve dalgaboyu arasındaki ilişkileri belirleyen temel tabiat sabiti Planck sabitidir.
Klasik fiziğin çıkmazlarından: “Kara cisim” ışıması
Klasik fiziğin anlayamadığı, kuantum mekaniğine giden yolu gösteren ilk büyük sorun “kara cisim” ışımasıdır.
Bu “kara cisim” terimi biraz yanıltıcı. Burada kastedilen madde ile termodinamik dengede olan radyasyon. Bu radyasyonun içinde bütün renklerden farklı miktarlarda var, bütün renklerden radyasyon enerjisi madde ile radyasyon arasında alınıp veriliyor ve gerek maddenin gerekse radyasyonun sıcaklığı sabit kalıyor. Böyle bir cismin sıcaklığa bağlı bir rengi de var, aşağıda göreceğimiz gibi bu renk kara falan değil.
Termodinamik dengede bir sistem düşünelim. Termodinamik denge demek bu sistemin her tarafı sabit bir T sıcaklığında, sistem çevresiyle enerji alışverişinde dengeye gelmiş, ne ısınıyor ne soğuyor, her atom ve molekülün ortalama enerjisi de kBT mertebesinde, sabit kalıyor demek. (Belli bir sıcaklığın enerji karşılığını belirleyen kB sabitine Boltzmann sabiti denir.)
Şimdi, termodinamik dengedeki cismimizdeki her atom ve molekülün enerjileri etraflarındaki diğer atom ve moleküllerle etkileştikçe anlık olarak değişiyor, fakat ortalama enerji sabit kalıyor. Her parçacık başka parçacıklarla etkileştiği gibi mutlaka elektromanyetik dalgalarla da sürekli etkileşiyor. Bu etkileşim Maxwell denklemleriyle iyice ayrıntılı olarak anlaşıldı.
Termodinamik dengede bütün atomların saniyede aldığı ve verdiği enerji miktarları eşit olmalı. Öyleyse T sıcaklığındaki bir sistemde elektromanyetik dalgaların da T sıcaklığına özgü özellikleri olmalı. Termodinamik dengede elektromanyetik dalgaların farklı frekanslarda ne kadar enerji taşıdığı da sıcaklığın belirlediği bir özellik olmalı.
Soba ısındıkça değişen renk
Işık, elektromanyetik dalgaların gözümüzün algılayabildiği bir çeşidi. Tüm elektromanyetik dalgaları göremiyoruz, gözümüz ancak belli bir frekans/dalgaboyu aralığında elektromanyetik dalgaları algılayabiliyor. Işığın frekansını biz renk olarak algılıyoruz.
Belli sıcaklıktaki bir cismin mesela kızgın bir sobanın belli bir rengi vardır. Isındıkça renk önce kırmızı olur. Daha sıcak bir soba turuncu daha da sıcaksa sarı, sarı-beyaz, beyaz-mavi (akkor) olur. Daha da yüksek sıcaklıklarda soba renksiz, siyah gibi görünür, çünkü artık gözümüzün algılayamadığı mor-ötesi (ultraviyole) frekanslarda elektromanyetik dalga yaymaktadır. Aslında herhangi bir sıcaklıkta çıkan ışığı renklere ayırarak her bir frekansta ne kadar ışınım olduğunu ölçebiliriz. Soba kırmızı görünürken renklere ayrıştırırsak yani spektrumunu gözlersek mavi, yeşil, sarı vs. tüm renklerde (frekanslarda) belli bir miktar ışınım olduğunu, bileşik rengi kırmızı olarak gördüğümüzü anlarız.
Termodinamik dengedeki cisimlerden alınan ışıma spektrumu 19. yüzyılda gayet ayrıntılı ölçülebiliyordu. Işımanın renklere dağılması her sıcaklıkta hep aynı biçimde tipik bir eğriyi izliyordu. Sıcaklık arttıkça spektrumda en baskın frekans artıyor, yani renk maviye, mora, morötesine doğru gidiyor ve toplam ışıma şiddeti (cismin tüm renklerde toplam ne kadar ışıdığı da sıcaklığın dördüncü kuvvetiyle T4‘e orantılı olarak artıyordu.)
Resimde farklı sıcaklıklarda ışıma spektrumları gösteriliyor.
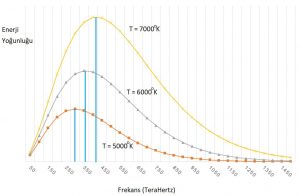
Bu ölçümleri klasik fizik ile anlamak mümkün değil.
Klasik fizik kullanarak bunu anlamaya çalışırsak, şöyle bir hesap yapılıyor. Önce sistemin içinde her bir frekansta kaç farklı dalga var bunlar sayılıyor. Aynı frekansta ama farklı yönlere giden kaç farklı dalga olabilir: frekansa $f$ diyelim dalga sayısı frekansla $f^2$ye orantılı olarak artar.
Peki farklı dalgaların her biri ne kadar enerji taşır?
Klasik fiziğe göre her farklı dalga, frekansı ne olursa olsun, aynı bir atom veya molekül gibi, ortalama $k_B T$ kadar enerji taşır. Şimdi her bir frekanstaki farklı dalgaların sayısı ile her birinin taşıdığı enerjiyi çarparsak, her frekanstaki enerji miktarının yani spektrumun formülü ($k_B T f^2$ ) ye orantılı olmalı, klasik fizik doğru ise. Bu da gözlenen spektruma uymamaktan öte çok saçma bir beklentiye yol açıyor: Bütün frekanslarda yayılan enerjiyi, yani $k_B T f^2$’leri toplarsak, frekans arttıkça katkılar artıyor ve sonunda, sıcaklık düşük de olsa farketmez, termodinamik dengedeki tüm cisimler sonsuz miktarda ışınım enerjisi yayarlar sonucu çıkıyor. Klasik fizik sonsuz saçma bir sonuç veriyor.
Klasik fizikteki hata nerede?
Klasik fizikte her farklı dalganın ortalama enerjisi $k_B T$ çıkar çünkü dalganın anlık enerjisi $E$ sıfırdan sonsuza bütün değerleri alabilir. 19. Yüzyıl sonunda Ludwig Boltzmann’ın gösterdiği gibi her bir enerji değerinin olasılığı $P(E)= C.\exp(-E/k_B T)$ formülüyle belirlenir. Bu formülün ne anlama geldiğini bilmiyorsanız önemli değil, önemli olan her bir enerji değerine ne sıklıkla rastlanacağını bildiren, deneylerle sıkı sıkıya doğrulanmış bir formülümüz var. Enerjinin bütün değerleri alabileceğini kabul ederek Boltzmann olasılık formülüyle ortalama enerji değerini hesaplarsak $k_B T$ çıkar.

1900 yılında Alman teorik fizikçi Max Planck çok radikal bir varsayımla sorunu çözdü: Dalganın enerjisi her değeri alamaz. Dalga parçacıklardan (kuantumlardan) oluşur ve bu parçacıkların her birinin enerjisi E dalganın frekansına orantılıdır. Yani
$E = hf$
Burada $h$ de şimdi adına Planck sabiti dediğimiz orantı katsayısı. Bu durumda her bir dalga her enerji değerini değil sadece $n$ = 0,1,2,3… vs kaç kuantum bulunduğuna göre $nhf$ enerji değerlerini taşıyabilir. Bunların da Boltzmann olasılık formülüyle ağırlıklı ortalamasını aldığımızda her bir dalga türünün termodinamik dengede taşıyacağı ortalama enerji artık $k_B T$ değildir. Ortalama enerji hem sıcaklık $T$ ye hem de frekansa bağlı içinde $h$ sabiti de bulunan daha karmaşık bir formülle ifade edilir.
Ortalama enerjiyi aynı frekanstaki dalgaların sayısını veren $f^2$ ile de çarpınca çıkan formül tam tamına deneyde gözlenen ışınım spektrumunu vermesin mi? Planck’ın hesapladığı formül gözlenen karacisim ışıması spektrumuna uyarlandığında sabitin değeri de $h$ = 6,3 .10-34 Joule.saniye olarak bulunuyor.
Planck böylece, dalgaların aynı zamanda parçacıklardan oluştuğu gibi kimsenin anlayamadığı bir varsayımla, termodinamik dengedeki ışımanın özelliklerini tam da gözlendiği şekilde hesaplamayı başardı. Nedeni anlaşılamasa da klasik fiziğin bu kadar kötü çuvalladığı temel bir sorunda gözlemlerle tamtamına uyan bir açıklama, herhalde doğru olmalıydı. Elektromanyetik dalgalar parçacıklardan yani kuantumlardan oluşuyordu, bu kuantumlara ‘foton’ diyoruz.
Işığın parçacık olma haline bir örnek daha: Fotoelektrik olay
Dalgaların, bu arada ışığın, $E = hf$ ilişkisine uyan parçacıklardan (kuantumlardan) oluştuğu fikri tamamen farklı bir dizi deneyin, fotoelektrik olayın açıklamasını da getirdi. Bir metale ışık gönderildiğinde metalden dışarı elektronların fırladığı gözleniyordu. Daha parlak ışık gönderilirse daha çok sayıda elektron çıkıyordu. Ama ışık ne kadar parlak olursa olsun çıkan her bir elektronun enerjisi değişmiyordu. Çıkan elektronların enerjisinin ancak ışığın frekansıyla arttığı gözleniyordu. Yani frekansı daha yüksek olan mavi ışığın aynı metalden çıkarttığı elektronlar, daha düşük frekanslı kırmızı ışığın çıkarttığı elektronlardan daha enerjikti. 1905’te Einstein fotoelektrik olayın Planck varsayımıyla açıklandığını gördü.
Metale gelen ışığın $E = hf$ enerjili her bir fotonu, enerjisini bir elektrona aktarıyor. Bu enerji bağlanma enerjisini ($B$) aşıyorsa elektron metaldan sökülüyor ve serbest kalıyor. Serbest kalan elektronun enerjisi
$E_{elektron} = h f – B$
oluyor. Yani belirli bir metalden çıkan elektronların enerjilerini artırmanın tek yolu frekansı arttırmak.
Fotoelektrik olayda çıkan elektronların enerjileri ile gelen ışığın frekansı (rengi ) $f$ arasında gözlenen ilişki tam da böyle. Böylece fotoelektrik olay deneylerinden elektronların o metale bağlanma enerjileri ile birlikte Planck sabiti $h$ nin değeri de kara cisim ışımasından tamamen bağımsız, apayrı bir bağlamda elde ediliyor ve yine aynı $h$ değeri bulunuyor. Demek ki Planck sabiti evrensel bir doğa sabiti. Planck sabiti başka birçok fizik olayında da önemli rol oynuyor.
Kuantum mekaniğinin atomun yapısını nasıl çözdüğünü takip eden yazılarda okuyabilirsiniz.
Atom nedir? I
Atom nedir? II – Bohr’un atom modeli
Ali Alpar
Bilim Akademisi üyesi
Sabancı Üniversitesi Mühendislik ve Doğa Bilimleri Fakültesi
 Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.






