Bir önceki yazıda atomun gerçek olduğunun nasıl anlaşıldığını ve atomların (+) yüklü çekirdek tarafından elektrik kuvvetiyle bağlı tutulan elektronlardan oluştuğunu gösteren Rutherford deneyini konuşmuştuk. Vardığımız noktayı tekrarlayalım: Elektronun çekirdekten mesafesine $r$ dersek her bir elektronla çekirdek arasındaki çekici elektrik kuvveti $1/r^2$’ye orantılı. Klasik fiziğe göre, ortaya çıkan atom modeli bir yıldızla etrafındaki bir gezegen ya da birbirine kütle çekimi kuvveti ile bağlı iki yıldızdan oluşan bir çiftyıldız sistemi ile aynı: çünkü kütle çekimi de iki nesne arasındaki uzaklığa $1/r^2$ gibi bağlı bir kuvvet.
Şimdi en basit atomu, Hidrojen atomunu düşünelim. Hidrojen atomunun çekirdeği (+ e) yüklü tek bir protondan ibaret. Bu proton Hidrojen atomunun (– e) yüklü tek elektronunu $F = K e^2/r^2$ elektrik kuvvetiyle çekiyor. Burada $K$ sayısal değeri birim sistemimize göre belirlenen bir sabit katsayı. Hareket halindeki elektron çekim yüzünden kaçıp gitmek yerine proton etrafında yörüngede bağlı kalıyor. Yörüngenin $r$ yarıçaplı bir daire olduğunu düşünelim. Geometriden daire üzerinde hareket için gereken ivmenin $a = v^2 / r$ şeklinde dairenin yarıçapı ve elektronun hızı $v$’ye bağlı olduğu çıkıyor.
Newton’un 2. Yasası, $F = ma$, elektronun kütlesi $m$ ise, protonla elektron arasındaki $F$ çekim kuvvetinin sebep olacağı ivme $a$’yı belirliyor. Bütün bunları bir araya koyarsak
$$\frac{K e^2}{r^2} = \frac{m v^2 }{r}$$
ya da
$$\frac{K e^2}{r} = m v^2~~~~~~(1)$$
sonucu çıkıyor.
Klasik fiziğin verdiği bu bir tanecik denklem, buna Denklem (1) diyelim. Ama burada iki özellik var, elektronun hızı $v$ ve yörüngenin yarıçapı $r$. Denklemimiz bunların ikisini birden belirleyemez: $r$’nin her değeri mümkün, yeter ki o $r$ değeri için elektronun hızı $v$ de denklemin verdiği kadar olsun. Yani klasik fiziğe göre atomlar her büyüklükte, her yarıçapta olabilir!
Elektronu bağlı olduğu atomdan koparıp çıkarmak için biraz uğraşmak, iş yapmak, enerji harcamak lazım. Ne kadar? $E = ½ m v^2$ kadar. Ama her $r$ ve ona uygun olmak kaydıyla her $v$ değeri olabildiğine göre atomun enerjisi de her değeri alabilir, klasik fiziğe göre.
Denklem (1)’in öteden beri bilinen analoğu (benzeri) kütle çekimi ile birbiri etrafında dönen iki yıldız için $r$ yörünge yarıçapı ile $v$ hızını birbirine bağlayan, $1 / r$’nin $v^2$’ye orantılı olduğunu söyleyen Kepler Yasası’dır. Yine bir denklemde iki bilinmeyen var, $r$’nin her değeri mümkün çünkü ona uygun bir $v$ değeri var. Peki gerçekte öyle mi, her yörünge büyüklüğünde, her enerjide çiftyıldız sistemleri gözleniyor mu? Bunun cevabı evet: ikisi birbirine çok yakın şekilde birbiri etrafında dönen çiftyıldızlar olduğu gibi neredeyse etraftaki komşu üçüncü yıldızlara yıldızlara ulaşacak kadar birbirinden uzak çiftyıldız sistemleri de var. Yakın olanlar tam da Kepler Yasası uyarınca daha hızlı kareket ediyorlar, birbirinden uzak eşyıldızlar ise daha yavaş gidiyorlar.
Peki atomlarda durum nasıl?
Atomların boyutlarını biliyoruz: katı veya sıvılarda atomlar birbirine değiyor. O zaman bir maddenin katı veya sıvı fazdaki yoğunluğunu atom kütlesine bölerek ya da buna eşdeğer olarak, Avogadro sayısını kullanarak, her santimetre küpte kaç atom olduğunu, buradan da her bir atomun hacmini ve yarıçapını bulabiliyoruz. Bu basit hesaplar 20. yüzyıl başında da yapılıyordu. Buradan her türlü maddenin atom boyutlarının hep birkaç Angstrom (1 Angstrom = $10^{-8}$ cm) mertebesinde olduğu bulunuyordu. Zaten farklı maddelerin $gm/cm^3$ olarak yoğunluklarının aşağı yukarı aynı olması da farklı atomların boyutlarının benzer mertebede olduğunu gösteriyor. Yani burada daha önce bahsettiğimiz çift yıldız sistemlerinden farklı bir durum var: atomun boyu her değeri alamıyor.
Elektronların atomlara bağlanma enerjileri ne kadar?
Kimyasal reaksiyonlar atom ve moleküller arasında elektron alışverişine dayanır. Reaksiyonlarda atom ve elektron başına alınıp verilen enerjiler de hep aynı mertebede, kabaca 1 – 10 eV (elektron-volt) kadar. Voltaj, birim elektrik yüküne denk gelen potansiyel enerjidir. Bir enerji birimi olan elektron-volt da bir elektronun 1 Volt potansiyel farkında sahip olduğu enerjiden başka bir şey değil. Tam da bu yüzden kimyasal reaksiyonlara dayanan piller 1 Volt, 1,5 Volt, 5 Volt gibi değerler taşıyorlar. Demek ki atomların boyutları ve içlerindeki elektronların enerjileri klasik fizikteki gibi, Denklem (1)’e göre olabilecek her türlü değeri değil sadece dar aralıklarda belli değerler alabiliyorlar. Klasik fiziğe kalsa 1 cm veya 1 m veya 1 km boyunda atomlar da olabilirdi, atomdaki elektronlar da hızlı giden bir TIR kadar da enerji taşıyabilirlerdi. Dünyanın böyle olmadığı apaçık.
Üstelik klasik fiziğe göre çekirdek tarafından çekilerek yörüngede tutulan elektron, her ivmelenen yük gibi elektromanyetik dalgalar salarak enerji kaybedecek ve bu yüzden çok kısa bir süre içinde çekirdeğin içine düşecek, böylece atom yok olacaktı. Atomların yapıları ve dengeleri ancak elektronların hem parçacık hem de, aynı zamanda, dalga oldukları fikriyle açıklanabildi. Danimarkalı fizikçi Niels Bohr’un öne sürdüğü bu yeni atom modeli atomların özelliklerini ve kararlı olmalarını açıklayabiliyordu.
Bohr Modeli
Niels Bohr klasik fizikte Newton’un 2. Kanunu’ndan ibaret olan Denklem (1)’e ilave olarak elektronun yörünge yarı çapı $r$ ile hızı $v$’yi ilişkilendiren ikinci bir fizik yasası önerdi. Bohr bu yasayı ilk önce, klasik teorik fiziğin kavramlarıyla düşünerek
$$m v r = \frac {n h} {2\pi}$$
şeklinde yazmıştı. Burada $m$ elektronun kütlesi, $mvr$ çarpımı da atom içinde yörüngede dönen elektronun dönme hareketini belirleyen ve zamanla değişmeyen, sabit kalan ‘açısal momentum’ özelliğiydi. Denklemin sağ tarafında $h$ daha önce Kara Cisim Işıması’nda Planck tarafından, Fotoelektrik olayını açıklamakta da Einstein tarafından kullanılan, o yıllarda yeni ve esrarengiz olan Planck sabitiydi. $n$ ise 1, 2, 3, 4, … gibi bir tam sayı idi. Planck’ın tepeden inme bir biçimde “bir elektromanyetik dalganın sahip olacağı enerji $E$ illa ki dalgaların frekansı $f$ den türetilen $h f$ ‘kuantum’unun bir tam sayı katıdır.” hipoteziyle Kara Cisim Işıması probleminin doğru çözümüne ulaşıldığını hatırlayalım. Aynı buna benzer biçimde Bohr da atomun içinde yörüngede dönen elektronun açısal momentumunun illa ki $h / 2 \pi$ sabitinin tam sayı katı olması gerektiğini öne sürüyordu. Bohr’un bu esrarengiz formülü aslında elektronların dalga özelliği taşımasıyla ilgili. Formülün bu dalga anlamı daha sonra Fransız fizikçi Louis de Broglie (dö Broyl )tarafından ortaya atılan $\lambda = h / (mv)$ ilişkisi ile belirginleşiyor. Buna göre elektron hem parçacık hem de dalgadır. Elektronun dalgaboyu $\lambda$ (lambda okunur), parçacık özelliği olan momentumu $p = mv$ ile işte bu de Broglie ilişkisi ile bağlıdır. Şimdi de Broglie ilişkisini kullanarak Bohr’un hipotezini dalgaboyu $\lambda$ cinsinden yazalım:
$$2\pi r = \frac{n h} {mv}= n \lambda~~~~~~~~~~~~~~~~~~~~ (2)$$
Bu denklem (2) ne diyor? Elektronun yörüngesinin uzunluğu olan $2\pi r$ içine tam sayıda dalgaboyu oturmalı diyor. Böylece elektronun dalgaboyu atomun büyüklüğünü belirlemiş oluyor.
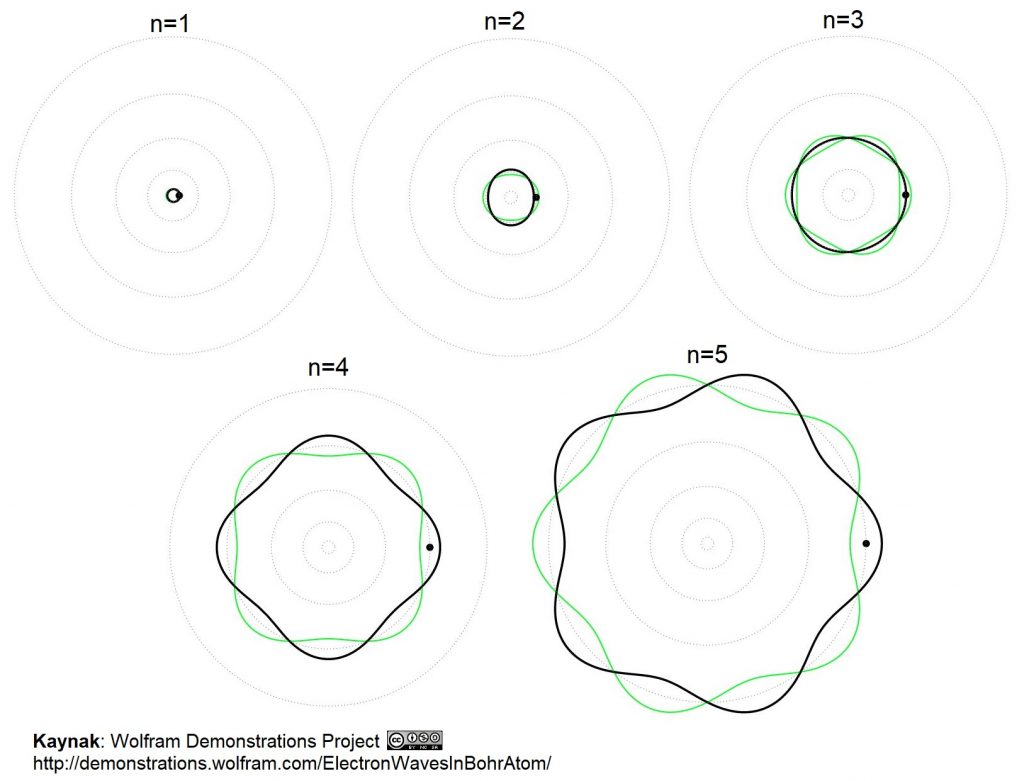
Tıpkı müzik aletlerinde olduğu gibi: küçük boydaki müzik aletleri en kısa dalga boylu titreşimleri barındırır yani en ince, tiz sesleri çıkarırlar, uzun dalga boylu pes (bas) seslerse en iri müzik aletlerinden çıkar: keman, viyola, çello ve kontrbası karşılaştırırsanız göreceğiniz gibi. Bunların hepsi de 50 cm – 2 m arasındaki boyutlardadır, çünkü kulağımızın duyduğu sesler için müzik aletlerinin tellerinde uyarılan dalgaların boyları da bu aralıktadır. Sadece tel titreşimleri değil her türlü dalga için dalga boyu ile dalgayı üreten sistemin boyutları benzer büyüklükte olur.
Bohr’un koyduğu Denklem (2) ile klasik fizikten gelen Denklem (1)’den iki bilinmeyen elektronun hızı $v$ ve yörünge çapı $r$ için çözümler elde ediliyor. Demek ki Bohr yaklaşımı, atomların neden sadece belli büyüklüklerde olduğunu açıklıyor. Elektronun yörüngesine kaç dalga sığdığına göre, yani $n = 1$ veya $n = 2$ veya $n = 3$ vs. için farklı yörünge yarıçapları (atomun farklı büyüklükte durumları) var. Her çözüm için de atomun belirli bir enerjisi var. Hidrojen atomunun $n = 1$ durumundaki yarıçapına Bohr yarıçapı deniyor. Bu yarıçapın değeri bu iki denklemden elektron kütlesi $m$, yükü $e$ ve Planck sabiti $h$ cinsinden $a_0 = 0.5$ Angstrom = $5 \times 10^{-11}$ metre olarak kolayca elde ediliyor. Hidrojen atomunun $n = 1$ durumundaki enerjisi de – 13.6 eV. Atomun herhangi bir $n$ durumu için enerjisi $E_n = – 13.6 eV / n^2$ , bu durumdaki atomun yarıçapı da $r_n = n^2 a_0$. Bu sonuçları kullanarak Hidrojen atomu bir enerji seviyesinden ($n$) başka bir seviyeye ($j$) geçerken aldığı ya da verdiği elektromanyetik dalgaların foton enerjileri ve frekansları bulunuyor. Bu frekans değerleri 19. Yüzyıldan beri spektroskopi deneyleriyle yani hidrojenden gelen ışığın tayfını (renklerini, frekanslarını) ölçerek hidrojenin sadece
$$f =\frac{13,6~eV}{h} \left[\frac{1}{n^2} – \frac{1}{j^2}\right]$$
şeklinde tam sayıların ters karelerinin farkına oranlı belli frekanslarda ışınım yaydığı veya soğurduğu biliniyordu. Bohr’un modeli tam tamına, tüm ayrıntısıyla bu formülü açıklıyor. Bu tesadüf olamazdı. Böylece elektronların dalga olduğu fikrinin doğru olması gerektiği ortaya çıktı.
Elektronun dalga olması atomların neden kararlı olduğunu yani klasik fiziğin beklentisindeki gibi elektronun ışınımla enerji kaybederek çekirdeğin içine inmediğini de gayet güzel açıklıyor: elektron bir dalga, en az bir tane dalgayı atomun içine sığdırması lazım, bu da atomun en az $n = 1$ durumundaki kadar büyüklükte olması demek. Dalgayı sığdırmak için atomun en az $a_0 = 0.5$ Angstrom = $5 \times 10^{-11}$ metre çapında olması gerek. Oysa atomun çekirdeği Rutherford deneyinin gösterdiği gibi $10^{-15}$ metre boyutlarında. Yani en küçük yörüngenin bile çapı çekirdeğin çapının 10 bin katı büyüklüğünde.
Böylece Planck ve Einstein’in dalga sanılan ışınımın aynı zamanda parçacık (kuantum) özelliği taşıdığı buluşundan öte parçacık sanılan elektronun da aynı zamanda dalga olduğu fikri Bohr modeliyle kanıtlanmış oldu. Demek ki bütün nesneler hem dalga hem parçacıktı. Parçacık özellikleri enerji $E$ ve momentum $p = mv$ dalga özellikleri olan dalgaboyu $\lambda$ ve frekans $f$ ile de Broglie’un $p = h / \lambda$ formülü ve Planck’ın $E = hf$ formülüyle bağlantılı.
Bohr’un atom modeli işin dalga özünü yakalamıştı. Ama doğru cevapları elde ettiği halde eksik bir modeldi. Bu dalga neyin dalgasıydı? Dalgayı tüm özellikleriyle elde edeceğimiz bir denklem olması lazım değil miydi? Bu soruların cevabı sonraki yıllarda elde edildi. Schrödinger ve farklı bir biçimde Heisenberg kuantum mekaniğinin temel denklemi olan Schrödinger dalga denkleminin buldular. Bu denklemin çözümü olan $\psi (x,y,z)$ dalga fonksiyonu da elektronun nerede olduğuyla ilgili bilgi veriyordu. Bir dalga ile betimlenen elektron herhangi bir anda belli bir yerde bulunmuyor, belli bir hıza ya da momentuma da sahip olmuyordu. Fizikçi Max Born dalga fonksiyonunun mutlak değer karesinin $|\psi (x,y,z) |^2$ şeklinde elektronun uzayda herhangi bir (x,y,z) noktasında bulunma olasılığını verdiğini öne sürdü. Bizim günlük dünyamızda, makroskopik ölçekte hiç farkında olmadığımız ve sezgilerimize tamamen ters düşen bu dalga özelliği maddenin yapısını anlamamız için temel şart. Bu dalga özelliğiyle tüm atomların yapısını ve periyodik tabloyu anlayabiliyoruz. Bunun nasıl olduğunu da başka bir yazıda ele alalım.
Ali Alpar
Bilim Akademisi üyesi
Sabancı Üniversitesi Mühendislik ve Doğa Bilimleri Fakültesi öğretim üyesi






