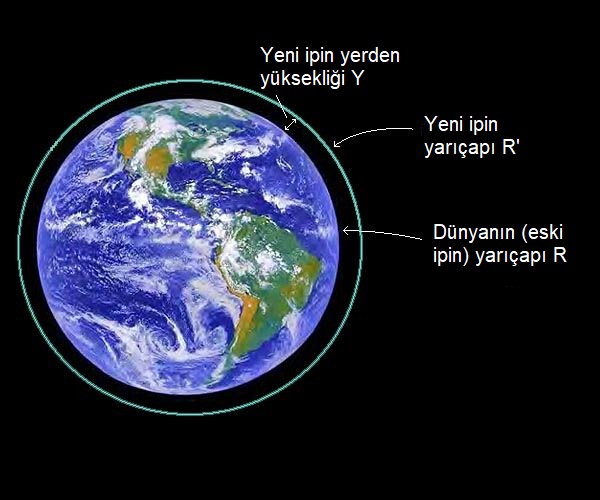
Dünyanın etrafını sıkı sıkı saracak bir ip bulalım ve saralım. Eğer dünyayı çevresi 40 bin kilometre olan mükemmel bir küre olarak düşünürsek ipin uzunluğu da 40 bin kilometre olacaktır. Şimdi bu ipi 1 metre uzatalım ve tekrar dünyanın etrafına saralım. İp daha uzun olacağı için doğal olarak biraz gevşek bir sarma olacak ve ip yerden belirli bir miktar yükseklikte olacaktır.
Bu yüksekliğin ne kadar olacağını tahmin edersiniz? Tahminizi aklınızda tutun.
40 bin kilometre ve 1 metre (m) karşılaştırılınca bu yüksekliğin çok çok az olacağı düşünülür, ama neye göre az?.
Basit bir geometrik model kullanarak çözelim. Dünyanın yarıçapına $R$ metre diyelim, ipin ilk uzunluğu $2\pi R$ olur. Şimdi ipe 1 metre ekleyince yeni yarıçap $R’$ olsun, böylece çevrenin değeri de $2\pi R’$ olur.
$$2 \pi R’=2\pi R + 1 m$$
$$2 \pi (R’-R)=1 m$$
Yeni durumda ipin yerden yüksekliği ($Y$) olsun. $Y$ yeni ve eski yarıçapların farkına eşittir, yani:
$$Y=R’-R$$
$$2 \pi (R’-R)=1 m$$
$$2\pi Y= 1m$$
$$Y=\frac{1m}{2 \pi} \sim 16 cm$$
Burada bulduğumuz 16 santimetre yeryüzündeki ölçeklere göre hiç de küçük bir değer değil. Ama 16 santimetreyi Dünya’nın yarıçapı olan 6300 kilometre ile karşılaştırmalıyız.
İşin ilginç yanı bu problemin yanıtının aldığınız kürenin boyutundan bağımsız olması, yani ister Jüpiter’in etrafını isterseniz bir portakalı sardığınız ipe 1 metre ekleyin, ip her defasında sarıldığı yere 16 santimetrelik bir gevşeklik ile sarılacaktır.