Yolda bir madeni para buldunuz ve hileli olup olmadığını merak ettiniz. Ne yapardınız? Sanırım ilk aklınıza gelen parayı bir sürü kez atıp yazılar ile turaların sayıları arasında bir denge olup olmadığına bakmak olurdu. Burada içgüdüsel olarak hissettiğiniz şey, para hileli değilse ve parayı çok kez atarsanız bunların yaklaşık olarak yarısının tura olacağıdır, ki bunun da olasılık teorisindeki ismi bu yazıda tartışacağımız büyük sayılar kanunu.
Beklenen değer
Beklenen değer kavramını gündelik hayatımızda sıklıkla duyuyoruz. Örneğin bir finansal aracın ya da şans oyununun beklenen getirisi, bir futbol maçındaki beklenen gol sayısı, vb. Matematiksel bir tanım verebilmek için ilk olarak rassal değişkenlerden bahsetmeliyiz. Gündelik hayatımızda belirli sayı değerlerini belirli olasılıklarla alan bir değişkene rassal değişken diyelim. Örneğin bir bankanın yarınki hisse senedi değeri, Fenerbahçe’nin bir sonraki maçında atacağı gollerin sayısı, okuduğunuz bu yazıyı dünya üzerinde sizden başka kaç kişinin okuyacağının sayısı! Her birinin içinde belirsizlik/rastgelelilik var, değil mi? Beklenen değer bu rastgelelikleri yorumlayıp ona göre kararlar almamıza yardımcı olan bir araç.
Rassal değişkenleri genellikle $X$, $Y$, $Z$ gibi büyük harflerle gösterdiğimizi not düşüp beklenen değeri tanımlayabiliriz. Bir $X$ rassal değişkeninin beklenen değeri $\mathbb{E}[X]$, $X$’in alabileceği değerleri ve bu değerlerin gerçekleşme olasılıklarını çarpıp ardından bunları toplayarak bulunur.
Örnek olarak adil bir zarı attığımızda elde ettiğimiz değere $X$ diyelim ve $X$’in beklenen değeri $\mathbb{E} [X]$’i bulalım. Bu durumda $X$, 1’den 6’ya kadar sayıların her birini 1/6 olasılıkla alacağına göre, beklenen değerimiz:
$$\mathbb{E} [X] = 1 \times \frac{1}{6} + 2 \times \frac{1}{6} +3 \times \frac{1}{6}+4 \times \frac{1}{6}+5 \times \frac{1}{6}+6 \times \frac{1}{6}=3,5$$
olacaktır.
Büyük sayılar kanunu
Adil bir zarı attığımızda elde ettiğimiz sonucun beklenen değeri olarak 3,5 bulduk. Peki bu tam sayı bile olmayan sayı bizlere ne anlatıyor? Bunu yorumlamanın birden fazla yolu olsa da bizler bulduğumuz 3,5’u, “zarımızı çok sayıda kez atarsak elde ettiğimiz sayıların ortalamasına yakın olacak değer” olarak yorumlayacağız. Bu örneği aklımızda tutarak artık büyük sayılar kanununun kabaca bir ifadesini verebiliriz.
Büyük sayılar kanunu: Büyük bir örneklem için örneklem ortalaması altta yatan rassal değişkenin beklenen değerine ‘yakın’ olacaktır.
Biraz daha matematiksel söylemek istersek $X_1,…, X_n$ belirli bir topluluğa dair bir bilgi tutan ortak beklenen değerleri $\mu$ olan (bağımsız ve aynı olasılık dağılımına sahip) rassal değişkenlerse
$$\frac{1}{n} (X_1+\cdots +X_n)$$
örneklem ortalaması $n$ arttıkça $\mu$’ya yaklaşacaktır.
Bu yazımızda işin teknik kısmından kaçındığımız için işin tarihsel boyutuna da giremeyeceğiz, ancak eğer girecek olsaydık Jacob Bernoulli, Emile Borel, Andrey Kolmogorov ve daha nice efsane ismin mutlaka önümüze geleceğini not düşelim.
Yazımızın başında yazı-tura üzerinden bir örnekten bahsetmiştik. Bu oldukça önemli, zira hayattaki hemen her şeyi zıtlıklar üzerinden modelleyebiliriz: bozuk/sağlam, iyi/kötü, başarılı/başarısız vs.
Bu tür ikili durumları temsilen yalnız 1 (başarı) ve 0 (başarısızlık) değerlerini alabilen bir $Y$ rassal değişkeni düşünelim. Herhangi bir denemede başarı olasılığı $p$ olsun. Bu durumda $Y$ rassal değişkeninin beklenen değeri
$$\mathbb{E} [Y]=1\times p+0\times (1-p)=p$$
olur. Yani beklenen değerimiz başarı olasılığımıza eşit çıktı. O halde bir örnek olarak tura olasılığının 0,4 olduğu hileli bir parayı 100 kez atarsak büyük sayılar kanunu elde ettiğimiz turaların oranının 0,4 civarında, elde ettiğimiz turaların sayısınınsa $0,4\times 100= 40$ civarında olacağını söylüyor.
Kasa kazanır!
Kumarhanelerdeki oyunların tasarımı ve bahis şirketlerinin oyunlara atadıkları oranlar gibi gündelik hayattaki bazı şans oyunlarının içinde büyük sayıları kanununun nasıl ortaya çıktığı şu an açık olsa gerek. Duruma özgü bir örnek olarak iki seçenekli bir kumarhane oyununda oyuncunun 0,2 olasılıkla 10 TL kazandığını 0,8 olasılıkla 3 TL kaybettiğini varsayalım. Bu durumda oyuncunun tek bir oyundaki beklenen kazancı
$$(0,2 \times 10)-(0,8\times 3)=-0,4 TL$$
olacaktır. Yani uzun vadede büyük sayılar kanununa göre kumarhane, ortalamada bir oyunda 40 kuruş kazanacaktır. Örneğin oyun 100 kez oynanırsa bu yaklaşık olarak 40 TL bir kazanç olacağını söylüyor. Kollu makineler gibi insanların başından kalkmadan sabaha kadar oynadığı basit bir makinenin dahi uzun vadede ne kadar çok para kazandıracağı buradan aşikar olsa gerek.
Burada altını çizmemiz gereken bir diğer nokta ise büyük sayılar kanununun deney az sayıda kez tekrarlanmışsa ortalamaya yaklaşık olacağımıza dair bir garanti vermediği. Örneğin, adil bir para ile oynanan bir yazı tura oyununda 20 kez üst üste tura geldiği zaman artık ortalamaya yaklaşmamız “gerektiği için” yazı gelme olasılığının arttığını düşünebilirsiniz ama aslında bir sonraki seferde tura gelme olasılığı halen 1/2. Bir başka deyişle böyle bir düşünce içine girerseniz “kumarbazın yanılgısı”nı yaşıyorsunuz demektir. “Monte Carlo yanılgısı” olarak da bilinen “kumarbazın yanılgısı” terimi 18 Ağustos 1918’de Monte Carlo kumarhanesinde gerçekleşmiş bir olayla ilişkili. Bu meşhur günde rulet oyunu üst üste tam olarak 26 kez siyah gelmiş ki bunun olasılığı 1/66,6 milyon.
Kumarhane örneğinde yasal bir yapının uzun sürede ortalamada para kazandığını görüyoruz. Ama yasadışı bazı durumlarda da büyük sayılar kanunu işe yarayabilir. Bir tane de alenen dolandırıcılık örneği görelim.
Alenen dolandırıcılık
Geleneksel bir şans oyunu ya da kumarhane oyununda oyunlar, oyuncunun da kazanma olasılığı çok düşük olmayacak şekilde tasarlanır. Örneğin sayısal loto gibi oyunlarda oyuncunun büyük ikramiyeyi olmasa da diğer ikramiyelerden birini kazanma olasılığı hatırı sayılırdır. Çünkü insanlar hiçbir şey kazanmama ihtimali çok yüksek olan bir işe girişmek istemez.
Bazı dolandırıcılık olaylarında ise hiç kazanma şansı olmamasına karşın kişiler bir oyunun içine düşebilir ve alttan alta büyük sayılar kanunu fikri gözlemlenebilir. Örneklendirelim.[1]DeGroot, M. H. ve Schervish, M. J. (2011) Probability and Statistics, Pearson,
4. Baskı.
Diyelim ki bir haftanın başında daha önce adını bile duymadığınız bir danışmanlık firmasından belirli bir meblağ karşılığında borsadaki hareketler için hizmet alabileceğinize dair bir e-posta alıyorsunuz. Firma, düzgün tahminler yapabildiğini kanıtlamak için belirli bir şirketin hisse senetlerinin bir sonraki hafta borsada artış yaşayacağına dair bir tahmin yollamış olsun. Her ne kadar bunun bir spam e-posta olduğunu düşünseniz de merakınızdan dolayı haftanın sonunda tahminin doğru olup olmadığını kontrol ettiğinizi ve mevzubahis şirketin hisse senetlerinin gerçekten de artış yaşadığını düşünelim. Üstüne, bir sonraki hafta da aynı firmadan benzeri bir e-posta geliyor ve tahmin yine doğru çıkıyor!
Bu durum yedi hafta boyunca böyle devam etsin; hafta başlarında firmadan bir tahmin geliyor ve her seferinde de doğru çıkıyor. Sekizinci haftanın pazartesi günü firmadan yine belirli bir meblağ karşılığında danışmanlık alabileceğinize ve bu tüyolar ışığında ciddi miktarlarda para kazanabileceğinize dair bir e-posta gelirse bu öneriye nasıl cevap verirdiniz? Ne de olsa son yedi haftadır yaptıkları tüm tahminler doğru şekilde sonuçlandı. Yani bir başka deyişle, tahminlerini tamamen rastgele yapıyor olsalardı, belirli bir hisse senedinin değerinin artmış veya azalmış olma olasılığını her tahminde bilme olasılıkları 1/2 olduğuna göre, tüm tahminleri bilme olasılıkları
$$\underbrace{\frac{1}{2}\times \frac{1}{2} \times \cdots \times \frac{1}{2}}_{7 \; \text{kez}}\approx 0,008$$
olurdu, ki bu da gerçekten büyük bir tesadüf gerektirirdi.
Tüyoları satın almadan önce dikkatli olmakta fayda var! Her ne kadar siz bu firmanın yaptığı tahminlerin sadece yedi tanesini görmüş olsanız da, firma çok sayıda (kolaylıkla milyonlarca) başka tahmini de eş zamanlı olarak yapıyor olabilir.
Bir örnek olarak firmanın bu sürece $2^7=128$ farklı olası müşteriye e-posta yollayarak başladığını varsayalım. İlk pazartesi günü, firma müşterilerinin yarısına belirli bir hissenin artacağını, diğer yarısına ise aynı hissenin düşeceğini söylesin. Bu durumda tam olarak 64 tahminleri doğru çıkacak ve dolayısıyla ikinci pazartesi günü doğru tahminde bulundukları 64 müşteriye tekrar aynı şekilde tahmin yollayıp bu kez 32 müşteride tahminlerini tutturacaklar. Yedinci haftanın sonunda ise firmanın kesin olarak bir tane tüm tahminleri doğru almış müşterisi olacak!
Firmamız diyelim ki bunu 10bin farklı 128şer kişilik grupla yapıyor. Her gruptan yedi haftada doğru tahmin götürülen insanların 1/10 olasılıkla daha fazla tüyo almak için “danışman” firmaya 100 lira yolladığını varsayalım. Büyük sayılar kanunu bize dolandırcı firmanın emekleri karşılığında ortalamada yaklaşık olarak
$$10000\times\frac{1}{10}\times 100 = 100000$$
lira kazanacağını söyler!
Bu eski bir hikayeydi ama modern dünyadaki birçok dolandırıcılıkta da benzeri bir durum söz konusu.[2]Buradaki konumuz “küçük sayılar kanunu” ve “harbiden büyük sayılar kanunu” ile ilişkili, belki bunlara başka bir yazıda döneriz. “Law of truly large numbers” Türkçeye yazar tarafından “harbiden büyük sayılar kanunu” olarak çevrilmiştir. İlgili referans: Diaconis, Persi, and Frederick Mosteller, Methods for studying coincidences, Journal of the American Statistical Association, 1989.
Daha da ilerisi: Monte Carlo yöntemleri
Büyük sayılar kanunu için benim favori örneklerimden birine geldik: Monte Carlo metodu. Çeşitli problemlere rastgele sayılar yardımı ile çözüm getiren yaklaşımlar genel olarak Monte Carlo metotları/yöntemleri olarak bilinirler. Bu yaklaşımın altında yatan fikir çok daha eskilere dayanmakla birlikte asıl kullanıma geçişinin 1940lı yıllar olduğunu belirtelim. Bu, bilgisayar teknolojisinin o dönemler geçirdiği süreçle ilgili – ve bir de tabii ki John von Neumann gibi bazı dahilerin o dönemler bu konuyla ilgilenmesiyle!

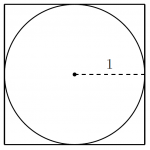
Burada Monte Carlo metoduna yönelik ufak bir hissiyat sağlamak için $\pi=3,141592…$ sayısına yaklaşık bir değer bulma üzerine basit bir örneğe odaklanacağız. İlk olarak Şekil 1’deki gibi bir karenin içine yerleştirilmiş yarıçapı 1 olan bir daire düşünelim.
Bu durumda karenin bir kenarının uzunluğu 2 olduğu için alanı 4, dairenin alanı ise yarıçap 1 olduğu için $\pi$ oluyor. O halde ikisinin alanlarının oranı
$$\frac{\text{Dairenin alanı}}{\text{Karenin alanı}}=\frac{\pi}{4}$$
Böyle bir durumda Monte Carlo yöntemi, ilk olarak karenin içinden çok sayıda rastgele nokta seçerek başlar (bir bilgisayar programı yardımıyla işlem kolayca gerçekleştirilebilir)[3]Bilgisayarınız yoksa yağmurlu bir havada bir leğen ve birkaç diğer şeyler sokağa çıkıp deneyi nasıl tasarlayabileceğini düşünmek de güzel bir alıştırma! ve bu noktalardan kaç tanesinin dairenin içine düştüğüne bakar.
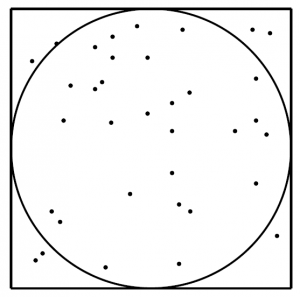
Sezgisel olarak dairenin içine düşen noktaların sayısının, karenin içindeki noktaların sayısına oranının şekillerin alanları oranı ile aşağı yukarı aynı olacağı ve dolayısıyla $\pi/4$ için yaklaşık bir değer vereceği düşünülebilir. Bir başka deyişle deneyde toplam $N$ tane nokta kullanıldıysa ve dairenin içine düşenlerin sayısı $M$ ise, $\frac{\pi}{4}\approx \frac{M}{N}$ olacağı için
$$4\times \frac{M}{N}$$
ifadesi $\pi$ sayısı için yaklaşık bir değer verir. Büyük sayılar kanunu kullanılarak $N$ sonsuza giderken $4\times \frac{M}{N}$ değerinin gerçekten de $\pi$’ye yakınsayacağı gösterilebilir. Bu da büyük $N$ değerleri için $\pi$’nin yakınlarında bir değere ulaşacağımızı söylüyor.
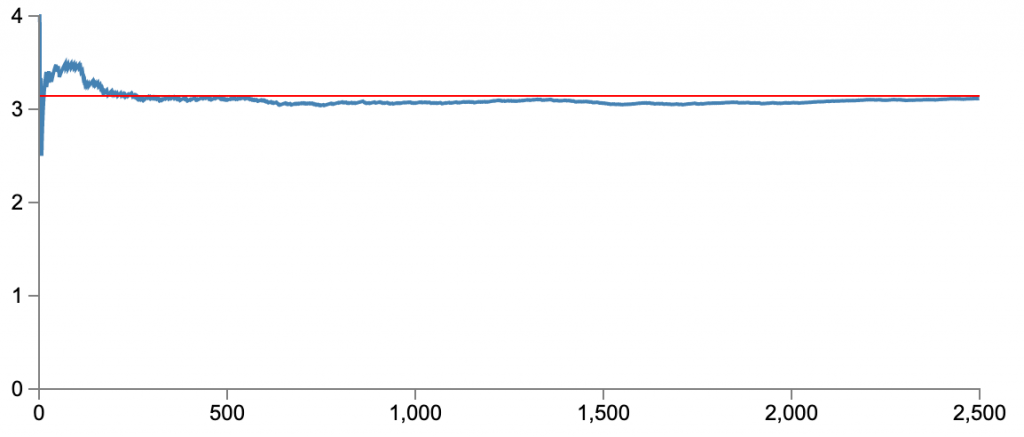
Bu deneyi https://graui.de/code/montePi/ sitesinden 2500 nokta çekerek yaptığımda 1946 tanesi çemberin içine düştü ve $\pi$ sayısı için bulduğum yaklaşık değer
$$4\times \frac{1946}{2500}=3,1136$$
oldu. Aynı web sayfasında 2500 deneme için elde ettiğimiz değerin $\pi$ sayısına yaklaşmasını gösteren grafiği oluşturabiliyoruz.
Çektiğimiz noktaların sayısını arttırarak daha da iyi yaklaşık değerler bulabiliriz. Her ne kadar burada biz sadece $\pi$ sayısının yaklaşık değerinin hesaplanmasını incelemiş olsak da, yöntem aslında çok daha zor problemlerin çözümleri için de kullanılabilir (örneğin çok katlı integrallerin hesaplanması gibi).
Kapanış
Yazının başına dönersek, bulduğumuz para adilse parayı çok ama çok kez attığımızda ortalamada yarısı kadar tura gelecek olmasına rağmen bu parayı kaç kez atarsak atalım hepsinin tura gelme olasılığı sıfır değil!
Elimizdeki sonlu bir örnekleme (ki gerçek hayatta durum hep böyledir) bakarak sonuçları değerlendirirken kesin olmasa da en azından olasılıksal bir şeyler söyleyebilmek isteriz. Geleneksel istatistiksel yöntemler de işte bu motivasyonla ortaya çıkmıştır. Bir sonraki yazımda büyük sayılar kanununun geleneksel istatistikteki güven aralıkları, hipotez testleri, $p$-değerleri ile ilişkisine dönmeyi ümit ediyorum.
Ümit Işlak
Boğaziçi Üniversitesi, Matematik Bölümü
Notlar/Kaynaklar
| ↑1 | DeGroot, M. H. ve Schervish, M. J. (2011) Probability and Statistics, Pearson, 4. Baskı. |
|---|---|
| ↑2 | Buradaki konumuz “küçük sayılar kanunu” ve “harbiden büyük sayılar kanunu” ile ilişkili, belki bunlara başka bir yazıda döneriz. “Law of truly large numbers” Türkçeye yazar tarafından “harbiden büyük sayılar kanunu” olarak çevrilmiştir. İlgili referans: Diaconis, Persi, and Frederick Mosteller, Methods for studying coincidences, Journal of the American Statistical Association, 1989. |
| ↑3 | Bilgisayarınız yoksa yağmurlu bir havada bir leğen ve birkaç diğer şeyler sokağa çıkıp deneyi nasıl tasarlayabileceğini düşünmek de güzel bir alıştırma! |