Bugün 29 Şubat.
Neredeyse her dört senede bir Şubat ayına eklenen artık gün.
Bu vesileyle bunun sebebini ve arkasındaki matematiği kısaca birlikte inceleyelim.
Artık yıl uygulamasının nedenini biliyorsunuzdur:
1 yıl Dünya’nın Güneş etrafında, 1 gün ise Dünya’nın kendi ekseni etrafında dönmesi için geçen süre. Fakat bir yıl bir günün tamsayı katı değil. Yani aslında 1 yıl tam 365 gün değil!
Aslında bakacak olursanız 1 gün ve 1 yılın süreleri de pek sabit değil. Ayın ve gelgitlerin etkisi ile günlerin süreleri değişiyor. Ama şimdilik bu kadar detaya takılmayalım.
Bir yıl yaklaşık olarak 365,24217 güne tekabül ediyor.
Yani Dünya’nın Güneş etrafında bir dönüşü süresince Dünya kendi etrafında 365,24217 defa dönüyor. İşte her yıl oluşan bu 0,24217 fazlalık 4 yılda birikip yaklaşık 1 gün ediyor.
Eğer mevsimlerin, ekinoksların ve astronomik olayların yıllar içerisinde kaymasını istemiyorsak 4 yılda bir, yıla 1 gün eklememiz gerekiyor. Bu da 4 yılda bir takvimlerimize eklenen 29 Şubat günü oluyor.
Öte yandan 4 yılda tam bir 1 gün değil, 4 $\times$ 0,24217=0,96868 gün birikmiş oluyor ve 1-0,96868=0,03132 yıl fazladan eklemiş oluyoruz. Bu küçük fazlalık 1/0,3132=31,92848… tane 4 yıllık döngüden sonra, yani 127,7139… yıl (yaklaşık 128 yıl) sonra fazladan bir gün eklemiş olmamıza neden oluyor. Demek ki 128 yılda bir, artık yıl ekleMEmemiz gerekiyor. 128 yıllık periyotların hesabını tutmak zor olduğundan bu süre yaklaşık 100 yıl olarak belirlenmiş ve her 100 yılda bir artık yıl eklemeden vazgeçilme kararı alınmış. 2000 yılı bir dördüncü 100 yıl olduğu için Şubat ayı 29 gündü. Ama 2100 yılında 28 gün olacak.
Daha bitmedi 😊 Yine de tam değeri elde edemediğimizden 400 yılda bir artık gün eklemekten vazgeçmekten de vazgeçmeye karar verilmiş. Bu şekilde 365 güne her dört yılda bir 1 gün ekleme, her 100 günde bir 1 gün çıkartma (eklenecek günü eklememe), her 400 günde bir 1 gün ekleme (eklenecek günü eklememekten vazgeçme) kararı alınmış ve bu şekilde 1 yıl ortalama
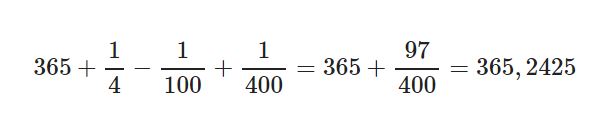gün olmuş. Gerçek süre olan 365,24217 güne epey yakın, ama tabii arada hala 0,0003299… günlük bir fark var, ki bu da yaklaşık 3030 senede 1 günlük bir fark yaratıyor. Hiç de fena değil. 🤔
Peki bundan iyisini yapabilir miydik?
Mesela yukarıda bahsettiğimiz gibi 100 yıl yerine 128 yıllık periyotlarla 1 gün eklememeyi seçseydik, ortalama
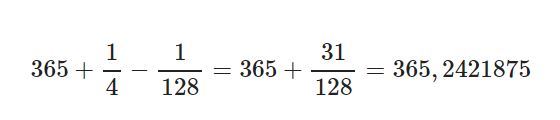
süren yıllar elde ederdik. Bu da gerçek süreden yalnız 0,0000175 gün fazla (hata yaklaşık 19’da 1’e indirilmiş oluyor).
Tabii 128’in katlarını hesaplamayı herkes istemeyebilir, bu sebeple 100 yıl uygulaması anlamlı olabilir. 128 yıl uygulamasını seçseydik 400 yerine 500 yılda bir düzeltme yapmak gerekecekti, yani
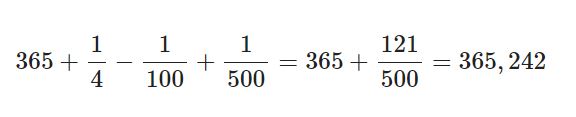gün süren yıllara denk gelecekti. Yani 0,00017 gün fark ile hatayı biraz daha azaltmış olacaktık.
Yine de 400 yıllık düzeltmelerinin seçilmiş olmasının farklı sebepleri olabilir. Bu takvim Papa XIII. Gregorius tarafından 1582 yılında uygulamaya konmuş ve günümüzde Gregoryen takvim adı ile anılıyor. 500 yerine 400 yılda bir düzeltme yapılmış olmasının sebebi o tarihte yıl ve günlerin sürelerinin bugünkü hassasiyetle bilinmiyor olması veya takvimin uygulamaya konulduğu 1582 yılının 400’e bölünen 1600 yılına yakın olması olabilir.
Ya 10 parmağımız olmasaydı
Peki 10 parmağımız olmasaydı ve artık yıl uygulamalarını 100, 400 gibi 10’un kuvvetlerine bölünen periyotlarla düzenleme gereği duymasaydık, ne yapardık?
Yukarıdaki hesaplardan gördüğümüz gibi 365,24217 sayısına yakın çok karmaşık olmayan kesirler bulmamız gerekiyor,
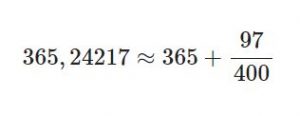örneğinde olduğu gibi.
Verilen bir gerçel sayıya yakın basit kesirler elde etmek için matematiğin bize sunduğu şahane bir yöntem var: sürekli kesirler.
Sürekli kesirler
Fikir çok basit. 365,24217 sayısını 365+0,24217 olarak yazalım. 1’den küçük olan 0,24217 yerine
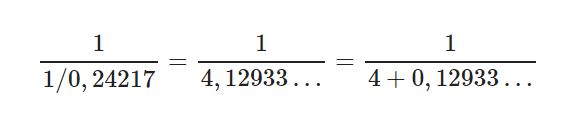yazabiliriz. Böylelikle
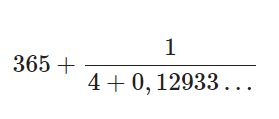
ifadesini elde ederiz. Yine 1’den küçük $0,12933\ldots$ için aynı yöntemi uygularsak
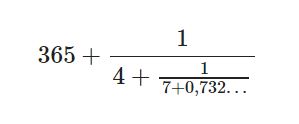
elde ederiz. İstersek bu süreci
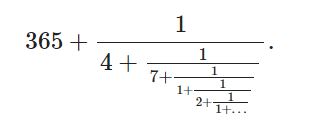
biçiminde devam ettirebiliriz. Peki ya sonra? Hep böyle gidecek mi?
Biraz hesap yaparsak paydalarda sırasıyla $4, 7, 1, 2, 1, 2, 1, 2, 1, 13, 3, 1$ sayılarını elde edeceğimizi ve sonrasında hesabın duracağını görürüz. Herhangi bir rasyonel sayı ile başladığımızda (365,24217 gibi) sonlu adım sonra bu işlem duracak. Buna sürekli kesir açılımı deniyor.
Bunu irrasyonel sayılar için yapmamızın önünde hiçbir engel yok tabii ki. Tek farkı rasyonel olmayan sayılarda bu sürecin sonsuza kadar devam edecek olması. Sürekli kesirlerin enteresan yanlarından biri işlemi herhangi bir adımda durdurduğumuzda, hesapladığımız sayıya (bu sayı irrasyonel de olabilir) yakın bir rasyonel sayı elde ediyor olmamız. Hatta elde ettiğimiz bu yaklaşık rasyonel sayının paydası bu rasyonel sayıdan küçük bütün kesirler arasında sürekli kesir açılımını hesapladığımız sayıya en iyi yaklaşık değer veren olduğunu göstermek mümkün (buradaki en iyi yaklaşık değerin tanımının detaylarına girmiyoruz).
Yukarıdaki örnekte
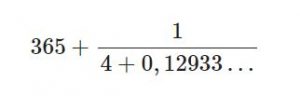
adımında $0,12933\ldots$ kısmını unutup süreci sonlandırdığımızda elde ettiğimiz $365+1/4=1461/4$ sayısı paydası 4’ten küçük bütün rasyonel sayılar arasında 365,24217 sayısına en yakın olanı. Devam ettiğimizde daha iyi yaklaşık değerler elde ederiz, sırasıyla
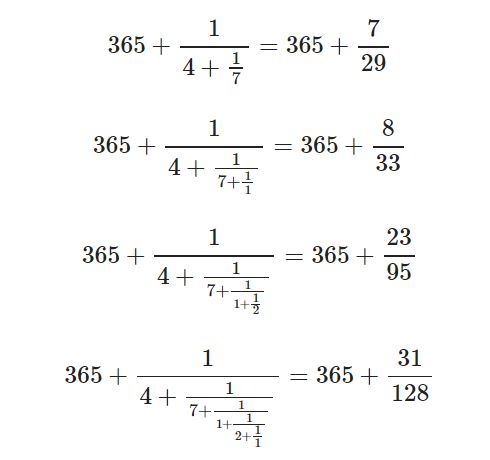
Buradan örneğin 29 yıllık periyotlarla düzeltme yapmanın (her 29 yılda bir 7 gün eklemenin) veya her 33 yılda 8 gün eklemenin (3 kere 4 yılda bir 1 gün, sonrasında 5 yıl sonra 1 gün eklemek) vs. kısa dönemli periyotlarla iyi yaklaşık değerler verdiğini görüyoruz. 33 yıllık periyotlarla yapacağımız düzeltmeler 0,00025 gün fark ile 400 yıllık düzeltmelerden daha iyi sonuç verecektir.
Yine de 100’ün katlarını seviyorsak (payda da 100’ün katlarını istiyorsak) bunu 365,24217 $\times$ 100 sayısının sürekli kesir açılımından elde ettiğimiz yaklaşık sayıları 100’e bölerek elde edebiliriz:
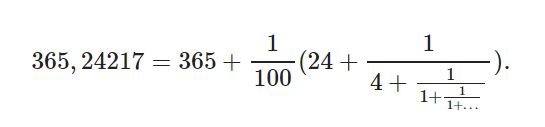
Buradan elde edeceğimiz yaklaşık değerler sırasıyla
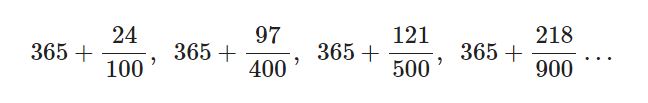
Bunlardan ilki 365+1/4-1/100 ifadesinden 4 senede bir artık gün eklemeyi ve 100 senede bir eklememeyi; ikincisi 365+1/4-1/100+1/400 bildiğimiz Gregoryen takvimi; üçüncüsü yukarıda bahsettiğimiz 400 yerine 500 senede bir düzeltilen Gregoryen takvim; 218/900 kesirinden gelen takvim ise 500 senede bir düzeltilen Gregoryen takvimin 4500 senede bir tekrar düzeltilmesi ile elde ediliyor.
Alp Bassa (Boğaziçi Üniversitesi, Matematik Bölümü)
Özer Öztürk (Mimar Sinan Üniversitesi, Matematik Bölümü)
Notlar/Kaynaklar:
Daha fazla detay için Yury Grabovsky’nin “Modern calendar and continued fractions” yazısını ve Emre Güngör ve Ülgen Kılıç’ın Matematik Dünyası Dergisi‘nin 102’inci sayısında yayımlanan “Sürekli kesirler” başlıklı yazısıyla birlikte okumanızı öneririz.
