Pek çok matematikçi, matematiğin kendi içerisinde bir güzelliğe sahip olduğunu veya olması gerektiğini düşünür. Zaten çalıştığınız işi seçecek kadar şanslıysanız, orada muhakkak bir güzelliği fark etmiş olmalısınız.

Ünlü İngiliz matematikçi G.H.Hardy 1941 yılında yazdığı ve “Bir matematikçinin savunması” başlığıyla TÜBİTAK tarafından yayınlanan otobiyografisinde, çevirmen Nermin Arık’ın ifadesiyle “Matematikçinin kalıpları da bir ressamın veya şairinki gibi güzel olmak zorundadır; düşüncelerse renkler ve sözcükler gibi uyum içinde olmalıdır. Güzellik ilk sınavdır. Çirkin matematik için dünyada kalıcı bir yer yoktur.” diye yazar.
Eğer bu kitabı daha önce okumadıysanız, matematikle uğraşın veya uğraşmayın, kuvvetle öneririm. C.P.Snow tarafından yazılan oldukça uzun önsözde Hardy’nin biyografisi veriliyor. Hardy’nin matematik hakkındaki denemelerini okuyunca matematiği sevmenin ne anlama geldiğini göreceksiniz.
Günümüzde her alanda bir yarışma açıp popülerliği, güzelliği, zenginliği vb. diğer özellikleri sıralamak moda haline geldiği için, matematikte de bir güzellik yarışması bulunuyor. Bütün yarışmalar gibi bu sıralama da ankete yanıt verenlerin ilgi ve bilgi alanlarına göre değişebildiği gibi, anketi hazırlayanların da sordukları sorulara bağlı olabilir. İngilizcede çok kullanılan bir ifade vardır: “Beauty is in the eye of the beholder”. Burada güzelliğin aslında sadece bakanlar tarafından oluşturulan bir kavram olduğu ima edilir, başka bir deyişle herkesin güzellik anlayışı farklıdır. Yani bir nevi “gönül kimi severse, güzel odur” veya “zevkler ve renkler tartışılmaz”.
Diğer yandan çoğu kimsenin hem fikir olduğu güzellikler de vardır. Matematiksel denklemler üzerinden yapılan bütün anketler, Euler denkleminin matematiğin en güzel denklemi olduğuna karar veriyor. (Matematiğin en şık denklemi, sarkac.org, Ekim 2017).
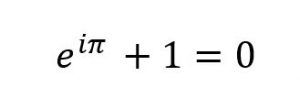
Bu sonuç birçok değişik ortamda tekrarlanmış ve artık kimse buna itiraz edip başka bir denklemi öne süremiyor.
Ama acaba ikinci en güzel denklem hangisi?
Anglo-Sakson yaşam biçimi tamamıyla birinci olmaya yönelik olduğu ve ikinciliği kaybetmekle eş değer tuttuğu için, bu soru karşısında çok fazla veri bulunmuyor.

Amerikalı popüler bilim yazarı Jim Holt’un 2018 yılında yayınlanan “When Einstein Walked with Gödel” isimli kitabı, matematiğin güzelliğine ait bir dizi denemesini de içeriyor. Holt, meşhur 4-renk problemini anlattığı kısımda 1988’de The Mathematical Intelligencer dergisinde yayınlanmış bir anketin sonuçlarına göre ikinciliğin de yine Euler’e ait olduğunu yazıyor. Ankette yazar okuyucularından en güzel teoremleri seçmelerini istemiş. 10 üzerinden yapılan değerlendirmede, Euler denklemi 7,7 puan alırken, Öklid’in asal sayıların sonsuzluğu teoremiyle Euler karakteristiği olarak bilinen denklem 7,5 puanla ikinciliği paylaşmışlar.
Öklid’in asal sayıların sonsuz olduğunu gösteren ispatı çok basit ve şıktır (25 Ekim’de güncellendi).
“Sonlu tane asal içeren bir liste alalım. Bunların hepsini çarpıp 1 ekleyelim. Elde edeceğimiz sayı (buna N diyelim) asal sayıysa listede olmayan bir asal sayı elde etmiş olduk. Eğer N asal değilse, o zaman N‘yi bölen en az bir asal sayı olmak zorunda. Bu asal çarpanına da p diyelim. p listedeki asallardan biri olamaz, çünkü bu durumda, hem N-1’i (listedeki asalların çarpımını) hem de N’yi bölecekti. Dolayısıyla bu iki sayının farkını, yani 1’i de bölmek zorunda olurdu. 1’i bölen bir asal sayı olmadığına göre p listedeki asallardan birisi olamaz. Dolayısıyla her iki durumda da listede olmayan yeni bir asal sayı (N veya p) elde etmiş olduk.” (Alp Bassa, Ayhan Dil ve Özer Öztürk, En büyük asal sayı, sarkac.org, Aralık 2018)
İkinci olan diğer denklem ise konveks (dışbükey) polihedronlar için Euler karakteristiğinin 2 olduğunu söylüyor:
V-E+F=2
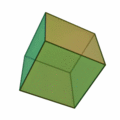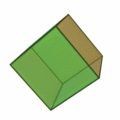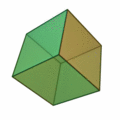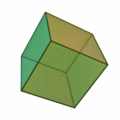

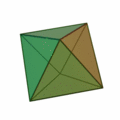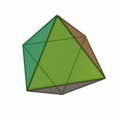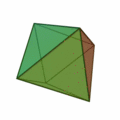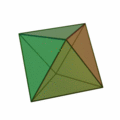
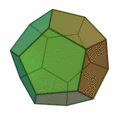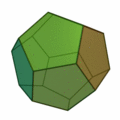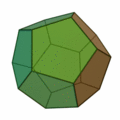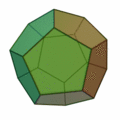
Polihedron, poligon yüzeylerle çevrelenen katı cisim demek. Bu denkleme göre konveks her polihedronda köşelerin (V-vertices) ve yüzlerin (F-faces) sayılarını toplayıp, kenarların (E-edges) sayısını çıkardığınız zaman hep 2 sayısını bulursunuz.
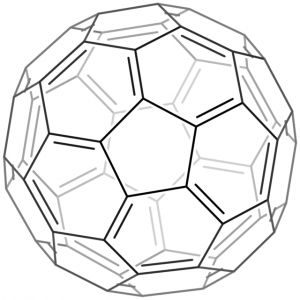
Daha uğraştırıcı olması nedeniyle fulleren için de, Euler karakteristiğinin 2 olduğunu okuyucuya bırakıyoruz. Fulleren, 1996 yılında R.F. Curl, Jr., H.W.Kroto ve R.E. Smalley’e Nobel ödülünü getirmişti. Karbonun grafit ve elmastan sonra kararlı üçüncü şekli olan ve aslında kömür tozunda bile bulunabilen fullerenin en bilinen hali C60’tır. 60 adet karbon atomu futbol topunu çok andıran ve “buckyball” diye de bilinen bu şekil 20 hekzagon ve 12 pentagonun birleşiminden oluşur.
Bu denklem içerisinde hiçbir delik olmayan cisimler için geçerlidir. Eğer cisminiz bir simit gibiyse, o zaman Euler karakteristiğinden, deliklerin sayısını 2 ile çarpıp çıkarmanız gerekir. Bu denklemi tartışan ilginç bir video (İngilizce).
Ayrıca polihedronun konveks olması, Euler karakteristiğinin 2 olması için yeterli şarttır ama gerekli değildir. Örneğin bir basketbol topunu birkaç noktada içine doğru bastırıp çukurlaştırırsak, konveks olma özelliği kaybolur ama hala Euler karakteristiği 2 olarak kalır. (Topoloji açıklamaları için Prof. Dr. Burak Özbağcı’ya teşekkürler.)
Ersin Yurtsever
Bilim Akademisi üyesi
Koç Üniversitesi Kimya Bölümü öğretim üyesi
David Wells, “Are these the most beautiful?”, The mathematical intelligencer, Vol.10, pp 37(1988)





