14 Mart Pi Günümüz kutlu olsun…
Pi ($\pi$) sayısı nedir merak ediyorsanız, $\pi$ sayısının sonsuza giden basamaklarını ezberlemeye niyetiniz varsa, $\pi$ sayısını mı Tau ($\tau$) sayısını mı desteklemek konusunda kararsızsanız veya $\tau$ sayısı da ne ola ki diyorsanız bu yazı size göre..
Pi sayısı nedir?
Herhangi bir çember için, çemberin çapı ($R$) yarıçapının ($r$) iki katıdır. Yani:
$$R=2 r$$
olur.
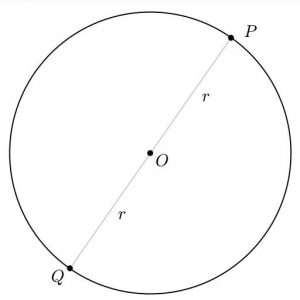
Çemberin sınırları boyunca uzanan mesafeye çemberin çevresi denir ve $Ç$ harfi ile gösterilir.
Çemberin şekline bakarak $Ç$ sayısının $2R$ sayısından büyük olduğu görebiliriz, çünkü P ile Q arasındaki çember üzerindeki mesafe (aynı biçimde Q ile P arasındaki çember üzerindeki mesafe) $R$ sayısından büyüktür. Bunun sonucunda da $Ç>2R$ olur. Eğer yeterince dikkatli bakarsanız $Ç$ sayısının $3R$’den büyük olduğuna bile ikna olabilirsiniz.
Eğer ki dairesel bir cismin çapını ve çevresini birbirleriyle kıyaslamak istiyorsanız cismin etrafını bir iple sarabilirsiniz. Sonra bu ipin uzunluğunu çapın uzunluğuna bölersiniz. Madeni bir parayı, bir şişenin altını, bir tabağı ya da devasa bir çemberi ölçmeniz fark etmez, hepsinde bulacağınız şey aynı:
$$Ç/R \sim 3,14 $$
Bu sayıya $\pi$ diyoruz. Yunan alfabesinde “p” sesini vermek için kullanılan bir harf olan $\pi$, “pi” diye okunuyor. $\pi$‘yi tamı tamına bir çemberin çevresinin, çapına oranı olan sabit sayı olarak tanımlıyoruz. Yani,
$$\pi = Ç/R$$
ve bu $\pi$ her çember için aynı!
Bunu bir çemberin çevresini veren bir formül olarak da yazabilirsiniz: $R$ uzunluğunda bir çapa ya da $r$ uzunluğunda bir yarıçapa sahip bir çember için;
$$Ç=\pi R ~~~~~\text{ya da}~~~~~ Ç=2 \pi r $$
olur.
$\pi$ sayısının kesirli bir sayı olmadığı, yani iki tam sayının oranı biçiminde yazılamayacağı biliniyor. Bu başka bir açıdan şuna denk, ondalıklı biçimde yazarsanız bu yazımda virgülden sonraki kısım bitmez (sonsuz ondalık basamaktan oluşur) ve birbirini tekrar eden bir yapıda devam etmez.
$\pi$ sayısından bahsederken söylemeden geçemeyeceğimiz bir şey daha var, $\pi$ sayısı aşkındır, yani rasyonel katsayılı hiçbir polinomun kökü değildir.
Geometri başta olmak üzere matematiğin hemen her alanında karşımıza çıkan $\pi$ sayısı ile ilgili daha bahsedecek çok şey var ama bugünün yani 14 Mart Pi Günü’nün hatırına biraz geyik yapalım.
$\pi$ Sayısını Anmak ve Ezberlemek*
İnsanların hayranlığı sebebiyle (ve süper bilgisayarların hızını ve duyarlılığını test etme metodu olmasıyla), $\pi$ sayısının trilyonlarca basamağı hesaplandı. Bu kadar basamak bilmeye kesinlikle ihtiyacımız yok. Sadece kırk basamakla gözlemlenebilir evrenin çevresini, en fazla bir hidrojen atomunun çapı kadar hata payıyla ölçebilirsiniz!
$\pi$ sayısı kendine neredeyse bir tarikat oluşturmuş durumda. Birçok insan 14 Mart Pi Günü’nde $\pi$ sayısını kutlamayı çok sever, ki bu gün aynı zamanda Albert Einstein’in de doğum günüdür.
Tipik bir Pi Günü, hem gösteriş hem de tüketim amaçlı hazırlanmış matematiksel temalarla süslenmiş pastalar, Einstein kostümleri ve tabii ki $\pi$ ezberleme yarışması içerir. Yarışmanın katılımcıları genellikle $\pi$’nin onlarca basamağını ezbere bilirler ve bu yarışmaların kazananının yüzlerce basamak ezberlemiş olması çok garip değildir. Bu arada, $\pi$ sayısının basamaklarını ezberlemede güncel dünya rekoru Hindistan’dan Rajveer Meena’ya ait, kendisi 21 Mart 2015 yılında $\pi$’nin 70 bin basamağını ezberden okumuştu! Guinness Rekorlar Kitabı’na göre, Rajveer Meena’nın bu basamakların hepsini ezberden okuması da yaklaşık on saat sürmüş.
İşte karşınızda $\pi$ sayısının ilk 100 basamağı:

Yıllar içinde insanlar $\pi$’nin basamaklarını ezberlemek için yaratıcı yöntemler geliştirdiler. Bir yöntem her bir kelimenin $\pi$’nin bir sonraki basamağını veren uzunlukta olduğu cümleler kurmaktır. Örneğin; “Sen o yolu o hızla uçabildin mi” cümlesinin kelimelerinin uzunlukları $\pi$ sayısının yedi basamağını verir: 3,141592
Etkileyici bir örnek 1995 yılında Mike Keith tarafından yazılmıştı; bu örnek 740 basamağı veriyordu ve aynı zamanda Edgar Allan Poe’nin “Kuzgun” adlı şiirinin bir parodisiydi. Sıfır sayısı için 10 harfli kelimeler kullanılmıştı. Keith daha sonra işi büyüterek, 3835 basamak veren “Cadaeic Cadenza” isimli bir eser, 10bin basamağı veren bir kitap da yazmıştı.
Ancak bu kelime uzunluğu metodunun ciddi bir problemi var. Cümleleri, şiirleri ya da hikayeleri ezberleyebilseniz bile, her bir kelimedeki harf sayısını hızlı bir şekilde belirlemek pek mümkün değil.
Hemen hemen bütün matematikçiler $\pi$ sayısının matematikteki en önemli sayı olduğu konusunda hemfikirdir. Ancak $\pi$ sayısını kullanan formüllere ve bunların uygulamalarına bakarsanız, göreceksiniz ki birçoğunda $\pi$ sayısı 2 ile çarpılmış bir şekildedir. Yunan alfabesi harflerinden $\tau$ (tau) bu değeri temsil etmek için kullanılır:
$$\tau=2\pi$$
Birçok kişi inanıyor ki; eğer zamanda geri gidebilseydik ve $\pi$ sayısını değiştirebilseydik, matematiksel formülleri ve başlıca trigonometrik konseptleri $\pi$ yerine $\tau$ kullanarak daha basit şekillerde ifade edebilirdik. Bu fikirler şık ve eğlenceli bir şekilde Bob Palais tarafından yazılmış “$\pi$ Yanlıştır!” ve Michael Hartl tarafından yazılmış “Tau Manifestosu” başlıklı makalelerde açıklanmıştı. Buradaki ana argüman, çemberlerin yarıçapları temel alınarak tanımlanması ve bir çemberin çevresini yarıçapı ile kıyasladığımız zaman $C/R=2\pi=\tau$ elde etmemiz. Bu akımın önümüzdeki onyıllarda nasıl gelişeceğini görmek ilginç olacak. $\tau$ sayısının destekçileri (kendilerine tauist derler) doğru olanın kendi fikirleri olduğuna ciddi ciddi inanıyorlar, ancak geleneksel gösterime de toleranslı davranıyorlar!
Şimdi $\pi$ sayısının ilk yüz basamağını aralarında boşluklar olacak şekilde vereceğiz. Dikkat edelim ki, $\tau$ sayısı 6 ve 28 sayıları ile başlıyor, bunların ikisi de mükemmel sayılar. Öz bölenleri toplamına eşit olan pozitif tamsayılara “mükemmel sayı” denir. Mesela 6=1+2+3, 28=1+2+4+7+14. Peki bu tesadüf mü? Tabii ki. Ama eğlenceli bir tesadüf.

*Bu yazı Arthur Benjamin’in Basic Books tarafından 2015 yılında basılan The Magic of Math kitabından uyarlandı. Yazının çevirisi Uğur Doğan’a ait. Yeri gelmişken bir müjde verelim, bu kitabın Türkçe çevirisi “Matematiğin Sihirli Dünyası” adıyla Nika Yayınevi tarafından Mart 2019’da yayınlandı.
Ayhan Dil
Akdeniz Üniversitesi Matematik Bölümü öğretim üyesi
(`Matematiğin Sihirli Dünyası” çeviri editörü)






