Doğum günü problemi, istatistik alanında çok bilinmekle beraber, duymamış olanlar için ilginç bir olasılık sorusudur. Birçok yerde “doğum günü paradoksu” olarak da geçer. Aslında paradoks yaratacak bir konu değildir. Ama insan beyninin özellikle üssel hesap yapmadaki güçlüğü soruya içgüdüsel olarak verilen yanıt ile hesabı doğru yapıp bulacağınız sonuçların farklılığını “paradoks hissini” ortaya çıkarıyor.
Soru basit:
N sayıda insanın katıldığı bir toplantıda, en az iki kişinin aynı doğum gününe sahip olma olasılığı nedir?
Artık yılı hesap dışında bırakırsak ve eğer bu toplantıda iki kişi varsa, olasılık
$$O_2 =1 \times \frac{1}{365}=\% 0.27 $$
Çünkü ilk kişinin doğum günü herhangi bir gün olabilir ve bunun olasılığı 1’dir. Diğeri için 365 seçenek olduğuna ve bütün günlerin eşdeğer olduğunu var sayarsak (her ne kadar mevsimlere ve aylara göre doğum istatistikleri değişse de) iki doğumgününün aynı gün olma olasılığı %0.27 olarak bulunur.
Şimdi eğer bu partide 20 kişi varsa iki kişinin doğumgünlerinin aynı gün olma olasılığı kaça çıkar?
Biraz tembellik edip içgüdümüzle yanıt vermek istersek, olasılığın 1/365’in 20 katından az olamayacağını ve muhtemelen biraz daha fazla olacağını düşünürüz. Bu da %5-6 gibi bir yanıttır. Çünkü 2 kişide bu olasılık 1/365 ve 365 kişide ise 1 olmalıdır. Beynimiz lineer düşünmeye alıştığı için doğrusal oranlama ile yanıt ararız.
Şimdi biraz çaba harcayıp doğru olasılığı bulmaya çalışalım. Grubumuz 3 kişiden oluşuyorsa, 2 kişide uyguladığımız yöntemi kullanamayız. Çünkü 3 çift oluşturabiliriz (1 ve 2; 1 ve 3; 2 ve 3; 1, 2 ve 3 numaralı kişiler) ve bunların hepsinin olasılıklarını toplamak gerekir. Bunun yerine, problemi başka türlü düşünelim.
Bir partide bulunan 3 kişinin doğum günlerinin hepsinin farklı olma olasılığı nedir?
İki kişinin doğum günlerinin birbirinden farklı olma olasılığı
$$P_2= \frac{365}{365} \times \frac{364}{365}$$
Olmalı. Üçüncü kişi için:
$$P_3= \frac{365}{365} \times \frac{364}{365}\times \frac{363}{365}$$
Olarak bulunur. Bu şekilde N=20 için olasılık:
$$P_{20}= \frac{365\times 364\times 363 ….\times 346}{365^{20}} $$
Ve herhangi bir N içinse olasılık
$$P_N= \frac{365\times 364\times 363 ….\times (366-N)}{365^N} $$
olarak bulunur.
Bu sayıyı değişik şekillerde hesaplamak mümkün. En kolayı bir Excel dosyasında her N için, farklı doğum günü olma olasılığını hesaplamak:
$$P_N=P_{N-1}\times \frac{366-N}{365}$$
Doğal olarak iki kişinin aynı gün doğma olasılığı olan $O=1-P$ dir. Bu şekilde 20 kişi arasında iki kişinin aynı günde doğma olasılığı %41 olarak bulunur. Bu da ilk tahminimiz olan %5-6’dan çok daha fazladır.
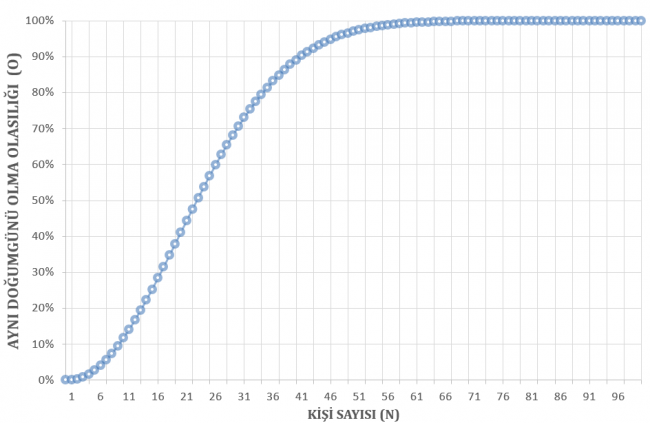
Grafik kişi sayısı ile bu olasılığın artışını gösteriyor. Artış lineer değil. 50 kişi için olasılık %97’yi buluyor. Şaşırdınız değil mi?
Ersin Yurtsever
Bilim Akademisi üyesi
Koç Üniversitesi Kimya Bölümü öğretim üyesi






