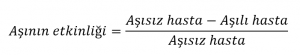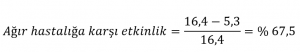2020 yılının ilk çeyreğinde hayatımıza hızlı bir giriş yapan COVID-19, aynı zamanda doğrudan ve dolaylı olarak pek çok kavramın da hayatımıza girmesine ve yeni tartışma alanları yaratmasına sebep oldu. Bu kavramların belki de en başında ise veri ve veriye bağlı (yorumlama, görselleştirme vb.) konular geliyor. Geçtiğimiz haftalarda The Guardian’da yayımlanan bir makaleden alıntı yapmak gerekirse “COVID-19’la beraber veriler de tıpkı el dezenfektanları gibi neredeyse artık her yerdeler.”[1]The Guardian. (13 Ağustos 2021) From Florence to the machines: The evolution of data journalism -in pictures. https://www.theguardian.com/gnmeducationcentre/gallery/2021/aug/13/the-evolution-of-data-journalism-in-pictures
Veriler de doğası gereği yanında her zaman istatistiği barındırır, çünkü verilerin toplanması, uygun yöntemlerle analiz edilmesi ve raporlanması aslında istatistik biliminin en genel tanımını oluşturur. Ancak bazen maalesef bilerek bazen de sehven verilerin yorumlanmasındaki süreç yanıltıcı sonuçlar doğurabilir.
Son zamanlarda özellikle gerek görsel basın gerek sosyal medyada ve COVID-19 ile ilgili çeşitli makalelerde ya da raporlarda en sık görülen başlıklardan biri “COVID-19 aşıları etkili mi?” Delta varyantının baskın hale gelmesiyle etkinliğinin nasıl değiştiği, hastalığın aşılılarda ağır hastalığa neden oluş ve hastaneye yatışları nasıl etkilediği bir merak konusu.
İsrail’den bir örnek
Yakın zamanda İsrail’den duyurulan bazı veriler Pfizer-BioNtech aşısının ağır hastalığı engellemediği kısacası “işe yaramadığı” yönünde yorumlandı. Ancak verilere daha dikkatli bakıldığında durumun hiç de böyle olmadığını görüyoruz. Perelman Tıp Fakültesi Biyoistatistik, Epidemiyoloji ve Enformatik bölümünden Jeffrey Morris bloğunda bu sorunu ele alarak İsrail’deki aşı ve hasta verileri üzerinden bir analiz yayınladı.[2]Morris, J. (26 Ağustos 2021). Israeli data: How Can efficacy Vs. severe disease be strong when 60% of hospitalized ARE VACCINATED? Covid Data Science. https://www.covid-datascience.com/post/israeli-data-how-can-efficacy-vs-severe-disease-be-strong-when-60-of-hospitalized-are-vaccinated Bu yazıda Morris’in analizini aşama aşama ele alarak inceleyeceğiz.
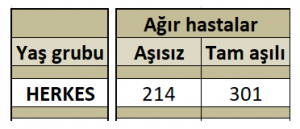
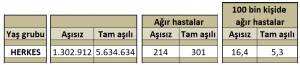
İsrail aşılama konusunda Dünya’da önde gelen ülkelerden, ancak son zamanlarda Delta varyantı etkisiyle vaka sayılarında dikkat çekici bir artış yaşıyor. İsrail Sağlık Bakanlığı’nın kapsamlı COVID-19 veri panelindeki 15 Ağustos 2021 tarihli verilere göre 515 ağır hastanın 214’ünün (% 41,55) aşısız, 301’inin (% 58,45) ise tam aşılı (İki doz Pfizer-BioNTech aşısı) olduğu görülüyor.[3]Analizde kullanmayacağımız için tabloda tek doz aşılanmış kişi sayısını dahil etmedik. Verilerin bütünü Morris’in yazısının sonunda mevcut.
Eyvah, ağır hastaların çoğu aşılı!! Bu aşılar işe yaramıyor mu demek?
Hayır. Verileri doğru sorular sorarak anlamlandırdığımızda aşıların işe yaradığını göreceğiz. Sormamız gereken ilk soru şu:
-
- Popülasyonda aşılanan kişilerin oranıyla aşısızların oranı aynı mı?
Aşı etkinliği analizi yalnız hasta sayıları üzerinden yapıldığında aşılama oranı düşükse aşı etkinliği olduğundan yüksek, aşılama oranı yüksekse aşı etkinliği olduğundan daha düşük çıkabilir.

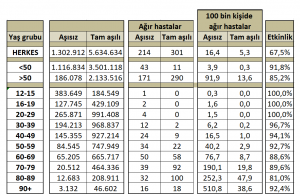
Aşılama oranını analize katmak için ağır hasta sayılarını 100 bin üzerinden yeniden hesaplayalım. Yani her 100 bin aşılı bireyin kaçı Covid-19’u ağır geçiriyor ve her 100 bin aşısız bireyin kaçı Covid-19’u ağır geçiriyor bulalım. Bunun için 15 Ağustos 2021’de İsrail’deki aşılı/aşısız sayılarına ihtiyacımız var.[4]Jeffrey Morris’in blog yazısının sonundaki veri dosyalarını kullandık. https://www.covid-datascience.com/post/israeli-data-how-can-efficacy-vs-severe-disease-be-strong-when-60-of-hospitalized-are-vaccinated
Tablodaki 100bin kişideki ağır hasta sayılarına baktığımızda aşısız kişilerin, aşılılara göre ağır hasta olma riskinin yaklaşık üç kat daha fazla olduğunu görüyoruz. (16,4/5,3 = 3,1)
Aşının ağır hastalığa karşı etkinliğini 100 bin kişideki ağır hasta sayıları üzerinden hesaplayacak olursak, ağır hastalığa karşı etkinliği % 67,5 olarak buluyoruz.
BONUS: Aşının etkililiği nasıl hesaplanır?
Aynı sayıda bireyin bulunduğu aşısız ve aşılı gruplarındaki hasta sayılarını “aşısız hasta” ve “aşılı hasta” olarak belirtelim. Aşı etkinliği şu şekilde hesaplanır:
Öyleyse 100bindeki ağır hasta sayılarını kullanarak aşının ağır hastalığa karşı etkinliğini bulabiliriz.
Daha önce İsrail’de yaygın kullanılan Pfizer-BioNtech aşısının Delta varyantına karşı etkinliği hastaneye yatışlarda % 95’in üzerinde bildirilmişti [5]Vaccines highly effective against hospitalisation from delta variant, https://www.gov.uk/government/news/vaccines-highly-effective-against-hospitalisation-from-delta-variant Biraz önce hesapladığımız % 67,5 sonucuna bakarak aşıların etkinliğinin azaldığı düşünülebilir, ancak bu da yanıltıcı ve yanlış olur.
“Gizli” karıştırıcı değişken: Yaş
İstatistikte iki değişken arasındaki ilişki incelenirken analizde olmasa da sonucu etkileyen ya da değiştiren karıştırıcı değişkenler (confounding variables) karşımıza çıkabilir.
ABD’den bir örnek; Florida, Michigan’a göre daha yüksek vefat oranına sahip bir eyalet. Ancak Florida’da Michigan’a göre yaşamın daha riskli olduğu gibi bir sonuca varmadan önce, yaş değişkenini hesaba katmak, Florida’daki yaşlı nüfus oranının çok fazla olduğunu ve vefatların da bu nedenle daha fazla olduğu bilmek, dikkate almak gerekiyor.[6]Confounding and Collinearity in Multiple Linear Regression, http://www.medicine.mcgill.ca/epidemiology/Joseph/courses/EPIB-621/confounding.pdf Yaş, burada karıştırıcı değişken.
İsrail örneğinde ağır hastalık ve aşı arasındaki ilişkiyi incelerken tıpkı Florida-Michigan örneğindeki gibi dikkatli bir şekilde hesaba katılmadığı zaman yanlış çıkarımlara neden olan “karıştırıcı” değişken ve buna bağlı çok sayıda faktör mevcut. İlk olarak bu faktörleri sıralayacak olursak;
-
- Ülkedeki aşılanmış nüfus oranının yüksek olması
- Yaşlı nüfusun neredeyse tamamının aşılanması
- Ülkede aşılanmayan kesimin çoğunluğunu gençlerin oluşturması
- Yaşlı nüfusun solunum yolu enfeksiyonu olma riskinin genç nüfusa göre fazla olmasını sayabiliriz.
Aşılama oranını en başında analize dahil etmiştik. Şimdi ise yukarıda hesaplanan %67.5’i bir daha masaya yatırıp karıştırıcı değişken olan “yaş”ı da hesaba katalım.
Literatürde karıştırıcı değişkenlerin etkilerini kontrol altına almak için çeşitli yöntemler mevcut, ancak en çok bilinen ve kullanılan yöntemlerden biri tabakalama (stratification). Yani, elimizdeki aşı ve hasta tablosunu yaş değişkenimize göre gruplara ayırmak, yaş değişkenine göre tabakalama yapmakla başlayabiliriz.
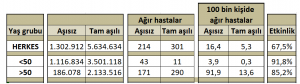
Eğer yukarıdaki ham veriyi genç (<50 yaş) ve yaşlı (>50 yaş) nüfusa göre yeniden gruplar ve daha sonra yaş gruplarına göre aşılı ve aşısız nüfus oranı ile 100.000 nüfus başına düşen hasta sayılarını yeniden hesaplarsak:
Aşının genç nüfusta (<50 yaş) ağır hastalığa karşı %91,8, yaşlı nüfusta (>50 yaş) %85,2 etkin olduğunu görüyoruz. Kısacası aşıların, varyantlara rağmen, hem genç hem de yaşlı nüfusta ağır hastalanmaya karşı yüksek koruma sağladığını, etkinliğinde bir azalma olmadığını söylemek mümkün.
Analiz sonucuna etki eden faktörleri sıraladığımızda yaşlı ve genç nüfus arasında aşılanma oranında dengesizlik olduğunu ve yaşlıların gençlere göre solunum yolu enfeksiyonuna yakalanma riskinin yüksek olduğunu söylemiştik. Bu yüzden 50 yaş sınırı ile oluşturulan genç ve yaşlı grupları aşı oranı ve ağır hasta olma açısından heterojen bir yapıya sahip. Eğer yaşa göre tabakalandırmayı daha dar yaş aralıkları kullanarak yaparsak, daha homojen gruplar elde edebilir ve analizimizin yol göstericiliğini arttırabiliriz. Bu adımı gerçekleştirdiğimizde ise 80-89 yaş grubu hariç (% 81,1) aşının etkinliğinin neredeyse tüm yaş gruplarında % 90’a yakın ya da % 90’ın üzerinde olduğunu görüyoruz.
Peki aynı veriden farklı farklı sonuç elde etmek nasıl mümkün oldu?
Bu sonuç karmaşasının ana sebebi Simpson Paradoksu olarak adlandırdığımız istatistik biliminin en ünlü olgularından biri aslında. Detaylı olarak[7]Simpson’dan önce bu olgudan Karl Pearson (1899) ve Udny Yule (1903) da bahsetmişti. ilk kez Edward H. Simpson’ın 1951 yılındaki “The interpretation of interaction in contingency tables”[8]Simpson EH. (1951) The interpretation of interaction in contingency tables. Journal of the Royal Statistical Society. Series B (Methodological);13(2):238–241 başlıklı makalesinde dile getirdiği ve 1972 yılında Colin R. Blyth tarafından Simpson Paradoksu olarak adlandırılan bu olguya göre bir ana veri kümesi kullanılarak iki değişken arasındaki ilişki incelenirken elde edilen sonuç, ana veri kümesi bu ilişkiye etkisi olan karıştırıcı değişken kullanılarak alt gruplara ayrıldığında ilk elde edilen sonucun tersi yönünde bir sonuç verebilir.Diğer bir deyişle bir veri kümesinden elde edilen sonuç, aynı veri kümesi alt gruplara ayrıldığında farklı olabilir.[9]Ameringer, S., Serlin, R. C., & Ward, S. (2009). Simpson’s paradox and experimental research. Nursing research, 58(2), 123–127. https://doi.org/10.1097/NNR.0b013e318199b517
Sonuç olarak İsrail verilerinde görüyoruz ki eğer aşı ve ağır hastalık arasındaki ilişkiyi incelerken karıştırıcı değişken olan yaşın etkisini dahil edilmezse, aşının etkinliğinin azaldığına dair bariz hatalı bir sonuç elde ediliyor.
Eldeki veri yaşa göre tabakalaştırıldığında ve doğru yüzdeler hesaba katıldığında aslında Pfizer Biontech aşısının varyantlara rağmen hala yüksek seviyede etkin olduğunu, daha doğrusu “çalıştığını” yani hayat kurtardığını görüyoruz.
Son söz, Simpson paradoksu aslında bizlere verilerin nasıl çarpıtılabileceğinin de bir örneğini sunuyor. O yüzden gerek Covid-19’la ilgili gerek başka alanlarda veriye bağlı sonuçları değerlendirirken sonuçları etkileyen tüm faktörleri dikkate almak, sonucun alt kırılımlarda da aynı olup olmadığını kontrol etmek ve sonrasında kesin bir sonuca ulaşmak önemli.
Ozancan Özdemir
ODTÜ İstatistik Bölümü
 Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. Görseller Wikimedia Commons’dan temin edilmiştir. İçerik kullanım koşulları için tıklayınız.
Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. Görseller Wikimedia Commons’dan temin edilmiştir. İçerik kullanım koşulları için tıklayınız.
Notlar/Kaynaklar
| ↑1 | The Guardian. (13 Ağustos 2021) From Florence to the machines: The evolution of data journalism -in pictures. https://www.theguardian.com/gnmeducationcentre/gallery/2021/aug/13/the-evolution-of-data-journalism-in-pictures |
|---|---|
| ↑2 | Morris, J. (26 Ağustos 2021). Israeli data: How Can efficacy Vs. severe disease be strong when 60% of hospitalized ARE VACCINATED? Covid Data Science. https://www.covid-datascience.com/post/israeli-data-how-can-efficacy-vs-severe-disease-be-strong-when-60-of-hospitalized-are-vaccinated |
| ↑3 | Analizde kullanmayacağımız için tabloda tek doz aşılanmış kişi sayısını dahil etmedik. Verilerin bütünü Morris’in yazısının sonunda mevcut. |
| ↑4 | Jeffrey Morris’in blog yazısının sonundaki veri dosyalarını kullandık. https://www.covid-datascience.com/post/israeli-data-how-can-efficacy-vs-severe-disease-be-strong-when-60-of-hospitalized-are-vaccinated |
| ↑5 | Vaccines highly effective against hospitalisation from delta variant, https://www.gov.uk/government/news/vaccines-highly-effective-against-hospitalisation-from-delta-variant |
| ↑6 | Confounding and Collinearity in Multiple Linear Regression, http://www.medicine.mcgill.ca/epidemiology/Joseph/courses/EPIB-621/confounding.pdf |
| ↑7 | Simpson’dan önce bu olgudan Karl Pearson (1899) ve Udny Yule (1903) da bahsetmişti. |
| ↑8 | Simpson EH. (1951) The interpretation of interaction in contingency tables. Journal of the Royal Statistical Society. Series B (Methodological);13(2):238–241 |
| ↑9 | Ameringer, S., Serlin, R. C., & Ward, S. (2009). Simpson’s paradox and experimental research. Nursing research, 58(2), 123–127. https://doi.org/10.1097/NNR.0b013e318199b517 |