COVID-19’un son birkaç haftada bütün dünyada küresel bir kriz haline gelmesiyle birlikte bu virüsü anlamak ve hasta kişiler için tedavi geliştirmek için bütün kaynaklar kullanılıyor. Bu çabalar her ne kadar epidemiyoloji ve tıp biliminin bir uğraşı olsa da COVID-19’un genel popülasyon üzerindeki yayılma mekanizması, sosyo-ekonomik etkisi ve buna bağlı alınacak kitle önlemlerinin öngörülebilmesi aslında matematikçiler tarafından çalışılıyor!
Matematikçilerin bu amaç için kullandıkları araçlardan bir tanesi de ağ bilimi! Ağ bilimi, matematiğin bir alt dalı olan graf teorisinin gerçek dünyadaki veriye uygulanmasıyla ortaya çıkmış bir araştırma alanı [1]. Ağ biliminin çalıştığı objeler ağlar! Ağ dendiğinde düşünmemiz gereken şey bir “noktalar” ve “kenarlar” kümesi yani graf!
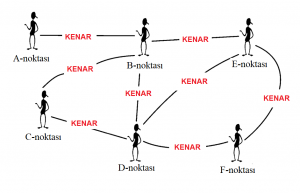
Ağ teorisine göre çeşitli insan dinamikleri bir ağ ile temsil edilebilir ve daha da iyisi, insan popülasyonu (noktalar kümesi) üzerindeki hastalık gibi bir etkileşim (kenarlar kümesi) (Şekil 1) çeşitli simülasyonlarla uzun vadeli tahmin edilebilir ve buna göre önlemler alınması sağlanabilir.
Bu yazıda ağlar üzerindeki en basit epidemik modellerinden olan SIR modelinin matematiğinden bahsedeceğiz. Bu basit modeldeki varsayımları anlatıp denklemleri çıkaracağız ve bu denklemlerden yapılabilecek çıkarımları anlatacağız. Yazının en sonunda da COVID-19’un da aktif olarak çalışıldığı SIRS ve SEIR modellerine de değineceğiz.
SIR Modeli
Diyelim ki popülasyonda hastalığın etkileyebileceği toplam birey sayısı N. SIR modeli olarak da bilinen modelin varsayımları şu şekilde:
Populasyondaki her birey üç harften biriyle temsil edilecek,
-
- S (Susceptible)- Hastalığa henüz yakalanmamış ve yakalanmaya açık sağlıklı bireyler
- I (Infected) – Enfekte olmuş/hasta bireyler
- R (Recovered/Removed) – İyileşen ve hastalığa bağışıklık kazanan veya hastalık yüzünden ölen bireyler
Bu gruplardaki birey sayıları zaman içinde değişecek fakat her anda S+I+R=N olmalı.
SIR modelinin iki aşaması var. İlk aşamada sağlıklı (S) bireyler hastalığa β hızıyla yakalanıyor. İkinci aşamada ise hasta (I) bireyler γ hızıyla iyileşiyor (veya ölüyor) (Şekil 2).
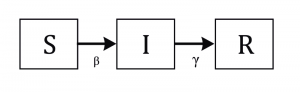
Burada tanıştığımız parametreler tanıdık olduğumuz olgularla ilişkili:
- β =her bireyin birim zamanda temas ettiği ortalama birey sayısı (a) x hastalığı bulaştırma olasılığı (b)
- γ ≈ 1 / hastalığın süresi
β ve γ parametrelerinin ikisi de sıfırdan büyük ve gerçek veriden kolayca hesaplanabiliyor.
SIR modelin uygulayabilmemiz için birkaç varsayımda bulunmamız gerekiyor:
- Popülasyon dış etkilerle değişmiyor; popülasyon doğum, ölüm (COVID-19 hariç) ve göç gibi etmenlere kapalı
- Hastalığın ömrü sınırlı
- Hastalığı atlatan bireyler hastalığa tam bağışıklık kazanıyor
- Virüsün kuluçka dönemi yok. Yani hastalığa yakalanan her birey hastalığı alır almaz başkalarını hasta edebiliyor.
Birinci varsayım çok gerçekçi olmasa da gerekli. İkinci varsayımı meraklılar için yazının sonunda notlar altında ele alıyoruz [2]. Üçüncü varsayımın COVID-19 için geçerli olup olmadığını bu yazının yayınlandığı tarihte bilmiyoruz ama geçerli olduğunu umuyoruz. Dördüncü varsayımın ise COVID-19 için geçerli olmadığını biliyoruz (kuluçka süresi 3-14 gün ve bu süre boyunca hastalığın bulaşmadığı düşünülüyor).
3. ve/veya 4. varsayımlar geçerli olmadığı durumda kullanılabilecek modelleri yazının sonunda tanımlayacağız.
SIR Modeli denklemleri
Bu varsayımlara göre SIR modelini aşağıdaki üç denklemle ifade edebiliriz. Bu denklemleri nasıl elde ettiğimizi aşağıda anlatacağız.
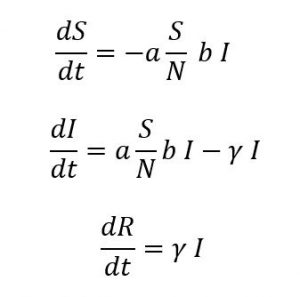
Öncelikle şunu belirtelim. Bu tür denklemlere diferansiyel denklem deniyor. Diferansiyel denklemlerin özelliği değişkenlerin değişim hızlarının değişkenlere bağlı olması. Sol taraftaki dS/dt, dI/dt ve dR/dt terimleri S, I ve R sayılarının olabildiğince sık zaman aralıklarıyla ölçülerek belirlenebilecek artış veya azalma hızlarını veriyor. ‘”Türev’’ denen bu ifadeler pozitif olursa artış negatif olursa azalma olur. Sağ tarafta a, b, γ katsayıları pozitif sayılar olduğundan (-) işaretli terimler azalmaya, (+) işaretli terimler artışa katkı yapıyor.
- Birinci denkleme göre sağlıklı insanların sayısı hasta olanların sayısı arttıkça azalacak. Hasta kişiler (I), birim zamanda a tane kişiyle hastalık bulaştırabilecek kontak kuruyorlar, bu kontakların S/N kadarı sağlıklı bireyler oluyor ve onları b olasılıkla hasta ediyorlar. Böylece S’nin azalma hızı hem I hem de S’ye bağlı oluyor.
- İkinci denklemde hasta sayısının değişim hızında iki etken var. Birinci etken hasta sayısının değişimi, hızını arttırıyor. Bu sağlıklı bireylerin hasta olmasından kaynaklanan artış yine hem S hem de I’ye bağlı. Bunu dengeleyen ikinci terim ise hasta sayısının değişim hızını azaltıyor ve artık hastalıktan kurtulan ve başka insanları hasta edemeyecek bireylerin etkisi.
- Üçüncü denkleme göre ise hasta insanların iyileşme hızı, hasta insan sayısıyla doğru orantılı hatırlayın ki γ pozitif bir sayı.
- Son olarak S + I + R = N ve de S, I, R bu altgruplara ait toplam insan sayısı.
Böylece S’nin azalma hızı hem I hem de S’ye bağlı oluyor.
Şimdi bu denklemleri S, I ve R gruplarının popülasyondaki oranları için yazalım ki hesap daha kolay olsun. Yani s=S/N, i=I/N ve r=R/N ve s+i+r=1 olacak şekilde yeniden düzenleyelim. β =ab, hastalığın bulaşma hızı
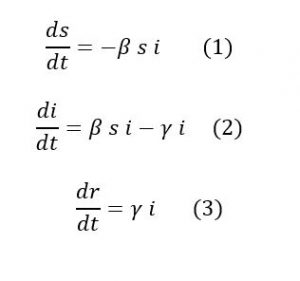
geçirmiş insanların oranı olan r(t) ilk zamanlarda üssel olarak (katlanarak) artıyor. En sonunda ise yine üssel sönümle belli bir doyum oranına yaklaşıyor. Arada basit üssel artışı sonundaki üssel sönüme bağlayan bir geçiş süreci var. Süreç içinde hastaların oranı da önce üssel olarak artıyor, sonunda üssel olarak sıfıra iniyor. Hiç hasta olmamış sağlıklıların oranı ise süreç boyunca azalarak sonunda küçük bir oranda sabitleniyor.
SIR Modelinin çözümleri
(1) ve (3) nolu denklemleri kullanarak yeni bir denklem edebiliriz: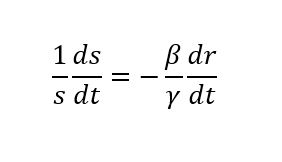
İki tarafın da salgının başlangıcı olarak kabul ettiğimiz bir andan (t=0) başlayarak integralini alırsak (integralini almak anlık değişimleri toplararak belli bir t zamanında ulaşılacak son s(t) ve r(t)’yi bulmak demek) aşağıdaki denklemi elde ediyoruz :
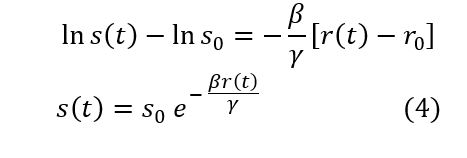
sonuçlarını elde ederiz.
İlk andaki (t=0 anındaki) değerler s0 ve r0 ile gösteriliyor. Burada ilk anda r grubunda kimsenin olmadığını kabul ediyoruz. Yani r0= 0.
Hatırlarsanız s+i+r=1, yani i=1-r-s. Bildiklerimizi denklem (3)’e geri koyalım:
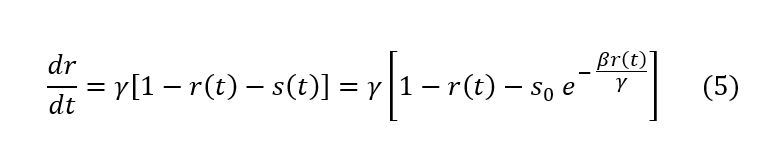
Sadece r(t) için bir denklem elde ettik. Bunu çözebilirsek r’nin zaman içinde nasıl değiştiğini bileceğiz. r ve s’nin bağlantısını denklem (4)’ten biliyoruz. i=1-r-s olduğuna göre bütün bu gruplardaki birey sayısının zaman içindeki değişimlerini bulabiliriz.
Denklem (5)in çözümü kolay olsa da elde edebileceğimiz integrali kapalı formda hesaplamamız mümkün değil. Numerik metotlarla yani bilgisayar yardımıyla bu denklemleri çözdüğümüzde s, i ve r için aşağıdaki gibi çözümler buluyoruz.
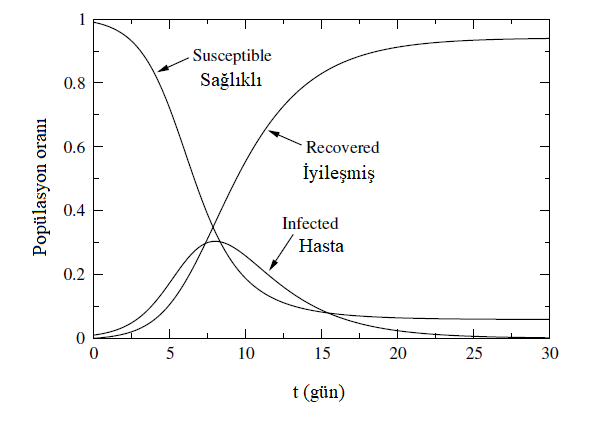
Şekil 3 de dikkatimizi çekecek birkaç şey var.
- S bireyler I bireye dönüştükçe S’lerin popülasyondaki oranı monoton bir şekilde azalıyor ve R’lerin popülasyondaki oranı monoton bir şekilde artıyor. I’lerin oranı ise başta biraz artsa da zamanla azalıyor.
- Bir başka ilginç gözlem ise S’lerin oranı 0’a gitmiyor çünkü belirli bir zaman sonra popülasyonda hasta birey kalmadığı için daha fazla bireyi hasta edemiyor. Yani popülasyonun bir kısmı hastalığa yakalanmadan epidemiği atlatabiliyor.
- R’nin uzun zaman geçtikten sonraki değerinin önemli bir anlamı var: Hastalık ortaya çıktığı andan itibaren hastalığa yakalanmış, herhangi bir zaman aralığında I olmuş bireylerin sayısı yani epidemiğin bilançosu!
Uzun zaman sonunda dr/dt=0 olacak, yani sayıların artık değişmediği durum. Denklem (5)’i kullanarak epidemiğin bilançosunu bulabiliriz.
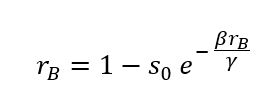
Çok büyük popülasyonlar için (örneğin dünya nüfusu) yani N sonsuza giderken, s0 yaklaşık 1 olacak. Dolayısıyla epidemiğin bilançosu için aşağıdaki ifadeyi bulabiliriz:
- R ilk başlarda üssel artış gösteriyor. En sonunda üssel sönümle hastalığı geçirenlerin bilançosu olan RB sayısına ulaşıyor. Aradaki evrede model üssel artıştan doyuma nasıl ulaşıldığını gösteriyor. Hasta sayısı I ise ilk başta üssel olarak, katlanarak artıyor, en sonunda üssel olarak azalıyor, arada geçiş sürecinde en yüksek sayıya ulaşıyor.
El yıkama/sosyal mesafenin önemi ve epidemik eşiği
Epidemiğin bilançosu için bulduğumuz ifadeyi aslında β/γ’nin bir fonksiyonu olarak görebiliriz. Öyle ki β≤γ ise epidemiğin bilançosu 0’a yaklaşacak. Bunun anlamı uzunca bir zaman geçtikten sonra hastalığın toplam seyri boyunca popülasyonun bir kısmı herhangi bir şekilde hastalığa yakalanmadan bu süreci atlatabilecek.
Bu bir anlamda akla yatkın, çünkü β≤γ olursa, hastalığa yakalanan kişilerin iyileşme hızları hasta olmayan kişilerin hastalığa yakalanma hızından daha büyük olduğu için belirli bir süre sonra hastalık azala azala kaybolacak.
Bu ne yazık ki hastalığın öldürücülüğü hakkında bir şey söylemiyor. COVID-19’a neden olan SARS-CoV2’nin kuzeni SARS virüsünü düşünün. 2003’ten beri bu virüs ortalıkta olmasına rağmen hastalığın bulaşıcılığı çok düşük olduğundan (yani β çok küçük), bu hastalık epidemik kategorisine erişemedi ve küresel bir kriz haline gelmedi. Buna rağmen bu hastalık yüzünden insanlar öldü ve halen ölümler oluyor.
Ancak hasta bireylere uygulanan karantina aynı şekilde devam ettiği sürece birkaç yüzyıl içinde belki de SARS virüsünün insan popülasyonu üzerinden temizleneceğini öngörebiliriz (hasta olan herkes birdenbire iyileşseydi veya hayatını kaybetseydi, hastalığı bulaştıracak yeni birey kalmadığı için hastalık yok olacaktı.)
Tam tersi durumda yani β > γ olduğunda bütün popülasyon patojenden etkilenmiş olacak, yani popülasyonun bir kısmı iyileşecek ancak bir kısmı da ölecek (hatırlayın ki R bireyler hastalıktan ölüm dahil bir şekilde kurtulanları temsil ediyor). Yani uzun süre boyunca eğer her an hasta olan insanların oranı iyileşen insanların oranından büyük kalırsa kaçınılmaz son olarak hepimiz bu hastalığa bir kere yakalanacağız.
Bu demek oluyor ki eğer β’yı yani bireylerin hastalığa yakalanma hızını düşürebilirsek, epidemiği kontrol altına alabiliriz. Bu iki rejim arasındaki ince çizgi β = γ olduğunda çiziliyor ve bu nokta epidemik eşiği olarak tanımlanıyor.
Eğer epidemik eşiğinin üzerindeyseniz, zaman sonsuza gittikçe, yeterli zaman geçtikten sonra, popülasyonun tamamı hastalıktan etkilenecek. Ama eğer epidemik eşiğin altındaysanız zaman sonsuza gittikçe hastalık popülasyondan temizlenecek.
Yani alınan bütün bu kitle önlemleri, okulların tatil edilmesi, büyük buluşmaların iptal edilmesi, sınırların kapatılması veya bireysel önlemler ellerin sık yıkanması çok önemli. Epidemiğin eşiğin altında kalmak için bunlar şart!
Ne de olsa β=ab; yani kontak kişileri (a) azaltmak (sosyal mesafe ve karantina) ve bulaştırma olasılığını (b) azaltmak (el yıkama vs) β’yı azaltıyor!
Daha karmaşık modeller: SIRS modeli ve SEIR modeli
SIR modelinde yaptığımız varsayımlardan birisi R olarak tanımladığımız bireylerin bir daha hasta olmayacağı, hastalığı geçirdikten sonra hastalığa tam bağışıklık kazanacaklarıydı. COVID-19 için bu yazının yayınlandığı tarihte henüz bu varsayımının doğruluğundan emin değiliz. Eğer hastalığa bir süre bağışıklık kazanılsa da iyileşen bireyler tekrar hastalığa yakalanabiliyorsa bu tip sistemler için SIRS modeli kullanılıyor. SIR modeli için tanımladığımız parametrelerin üzerine yeni bir δ parametresini hastalığı atlatan bireylerin hastalığa olan bağışıklıklarını kaybetme hızı olarak tanımlayacağız. O zaman SIRS modeli şu üç diferansiyel denklemle ifade edilebilir:
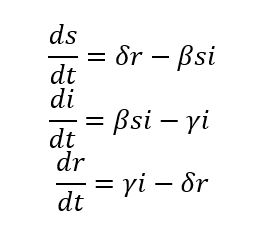
Ve yine s+i+r=1 geçerli.
- Birinci denkleme göre hastalığa yakalanmaya açık insanların sayısındaki değişim hasta olup hastalığı atlattıktan sonra bağışıklığını kaybeden bireyler tarafından artıyor ve hastalığa yakalanma hızıyla azalıyor.
- İkinci denklem SIR modeliyle aynı.
- Üçüncü denkleme göre ise hastalığı atlatan insanların sayısındaki değişim iyileşen insanların sayısıyla artıyor ve bağışıklığını kaybeden insanların sayısı ile azalıyor.
SIR modelinin aksine SIRS modeli analitik olarak çözülemiyor. Ancak lineer stabilite analizi ve diğer nonlineer teknikler kullanılarak analiz edilebiliyor. Numerik çözümler bu sistemin çok zengin bir dinamiği olduğunu gösteriyor. Örneğin hastalık epidemik halinde uzun süre devam edip daha sonra epidemik eşiğinin altına düşme eğilimi gösterebiliyor, bu rutini periyodik olarak tekrarlayabiliyor.
COVID-19’un bir kuluçka süresi olduğunu biliyoruz. Bu sürede hastalığı hasta olmayan bireylere bulaştıramayacağımız varsayılıyor [3,4,5]. Bu tür durumlarda kullanılan model SEIR modeli ve hastalığın seyir şeması şu şekilde (Şekil 4)
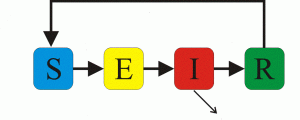
Buradaki adresten çeşitli parametreleri değiştirerek SEIR modeline göre hastalığın gidişatı öngörülebilir [6].
Son olarak bu modellerden literatürde çok fazla olduğunu ve değişik varsayımlar altında farklı modeller kullanmamız gerektiğini unutmayalım (örneğin aşı bulunduğunda SEIR modelinden de vazgeçip başka bir model benimsememiz gerekecek).
Epidemik modelleri hastalığın seyrini öngörebilmek için kullanılan matematiksel sistemler ve gerçek hayata kritik etkileri olabilir. Bu modellerdeki parametreler gerçek verilerle hesaplandığı için paylaşılan olguların şeffaflığı üzerine bir fikir verebilir. Konu tüm şeffaflığıyla anlaşılmadığında ekonomilere ve sağlık sistemlerine çok daha fazla yük olacaktır.
Ülgen Kılıç
Buffalo Üniversitesi – SUNY, Matematik Bölümü
Notlar/Kaynaklar:
[1] M.E.J. Newman, Networks: An Introduction, Oxford University Press, 2010.
[2] Herhangi bir T zaman aralığında γ’yi bildiğimiz sürece hastalığa yakalanan bir bireyin iyileşmeden önce ne kadar süre boyunca hasta kalacağını hesaplayabiliriz.
Herhangi bir verilen Δ t zaman aralığında bir bireyin iyileşme olasılığı (γ &Delta t) ve iyileşmeme olasılığı (1-γ Δt) olmalı. O zaman verilen Δt zamanından sonra hala hasta kalma olasılığı
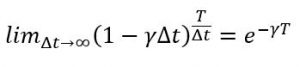
ve de T süresince iyileşmeyen bir bireyin T+Δt zaman aralığında iyileşme olasılığı p(T)dT
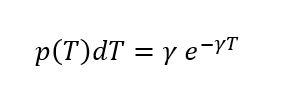
[3] Analysis and projections of transmission dynamics of nCoV in Wuhan https://cmmid.github.io/topics/covid19/current-patterns-transmission/wuhan-early-dynamics.html
[4] Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(20)30260-9/fulltext
[5] MRC Centre for Global Infectious Disease Analysis, https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/news–wuhan-coronavirus/
[6] Epidemic Calculator, http://gabgoh.github.io/COVID/index.html
