Düşünce yapımız büyük ölçüde deneyimlerimizden etkilenir. Örneğin birisi size “Köşede oturan beyaz fili düşünme sakın” dediği zaman ne yaparsanız yapın, kendinizi beyaz fili düşünmekten alıkoyamazsınız. Her ne kadar hayatınızda hiç beyaz fil görmemiş olsanız da fil, beyaz renk ve köşe gibi bildiğiniz kavramlarla hayalinizde aslında gerçekleşmesi olanaksız bir resim yaratırsınız.
Başka bir örnekte “0 ile 100 arasında birbirinden bağımsız bir sayı dizisi yaratmaya çalışın, yeni yazacağınız sayının, dizideki eski sayılarla hiç ilgisi olmasın. Diğer bir deyişle rastgele sayılar seçin.” denirse bunu yapmakta da aynı nedenle zorlanırsınız. Elinizde olmadan “çok çift sayı seçtim veya hep 50’den büyük sayılar aldım” diye düşünecek ve yeni seçeceğiniz sayıyı yönlendirmeye çalışacaksınız. Rastgele seçilmesi gereken dizi ne kadar büyükse, işiniz o kadar zorlaşır. Beynimiz böyle bir işi gerçekleştirmeye müsait değildir.
Neden böyle rastgele bir diziye ihtiyacımız olsun ki diye düşünebilirsiniz. Bugün pek çok bilimsel ve teknolojik problemi istatistiksel yollarla çözmeye çalışırız. Bunlar ekonomik bir modele etki edecek parametreleri incelemek olabileceği gibi, nükleer parçacıkların bozunmasından, proteinler etrafındaki su moleküllerinin yerini bulmaya kadar birçok farklı alanda, yüksek sayıda olayın incelenmesi ve bu olaylar arasındaki önemli bağlantıların bulunması olabilir. Bu tarz yaklaşımlara modelleme veya simülasyon diyoruz.
Doğru bir modelleme için, bilgisayar ortamında yaratacağımız çok sayıda olayın aslında önyargılarımızdan bağımsız (random, rassal, rastgele) olması gerekir. Aksi takdirde modelimize bilgilerimizi aktarırsak sonuçların zaten bildiklerimize benzer olması kaçınılmaz olur. Bu tarz rastgele sayıları (Random Numbers – RN) bilgisayar ortamında Rastgele Sayı Üreteci (Random Number Generator – RNG) dediğimiz algoritmalarla yaratabiliriz. Bu algoritmalar çeşitli teknikleri kullansalar da aslında Sözde Rastgele Sayı Üreteci (Pseudorandom Number Generator – PRNG) olarak bilinirler, çünkü hepsi az da olsa bir periyodiklik içerirler. Yine de insan beyninden çok daha bağımsızdırlar.
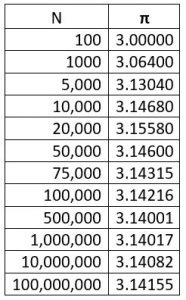
Rastgele sayıları kullanmak için küçük bir örnek verelim ve $\pi$ sayısını hesaplamaya çalışalım. Bunun için (0,0) noktası etrafında yarıçapı 1 olan bir daire düşünelim ve bu daireye teğet olan bir kare ekleyelim. Karenin köşeleri (-1,-1), (1,-1),(-1,1) ve (1,1) olur. Rastgele sayımızı (-1,1) aralığında alalım, bir çift sayı seçelim ve bu çift sayıyı da bir noktanın x ve y koordinatları olarak alalım.
Eğer x2+y2 birden küçükse nokta dairenin içinde, birden büyükse dairenin dışında kalır ama bütün noktalar karenin içerisinde olacaktır.Eğer bu noktalardan milyonlarcasını seçersek, dairenin içerisinde kalan noktaların sayısının toplam sayıya oranı, dairenin alanının karenin alanına oranını verecektir ki kolaylıkla $\pi$/4 olduğu görülür. Bu yöntem çok kolaylıkla uygulanabilir ama görülecektir ki, bu şekilde $\pi$ sayısına ulaşmak çok zahmetli bir yöntemdir. Tabloda görüldüğü gibi 3.141 sayısını bulmak için 100 milyon noktanın kullanılması gerekiyor. Daha önce bahsi geçen problemleri sadece bu tip bir hesap yaparak doğru bir şekilde modellemek hemen hemen olanaksız.
Monte Carlo yöntemi, rastgele sayıları akıllıca kullanarak bu yavaşlığı ortadan kaldırmak için önerilmiştir. 1953 yılında MR2T2 (ideal gaz parametreleri değil, yazarların soyadlarının baş harfleri: Metropolis, Rosenbluth, Rosenbluth, Teller, Teller) olarak bilinen makalede, rastgele olayların arasından önemli olanları seçerek ilerlemenin yolları gösterilmiştir. Kumar oynanan gazinosu nedeniyle meşhur olan Monte Carlo şehrine bir atıf yapılmaktadır. Örneğin 21 oynarken rastgele bir strateji kullanmak yerine, daha önce oynanan oyunlardan alınan bilgiler doğrultusunda olasılıklar belirlemek doğru olur. Sonunda karar vermeniz gene de rastgele olacaktır ama hangi durumlarda kazanma olasılığınızın ne olduğunu bilmeniz, size daha akıllı bir oyun planı sağlayacaktır. Tabii çıkan kağıtları sayarsanız, bu olasılıkları daha sağlıklı elde edebilirsiniz ama kumarhanenin de sizi dışarı atma olasılığı yüksek olur.
MR2T2 yöntemi, önem derecesine göre örnekleme olarak (importance sampling) bilinir. Bu yaklaşımda rastgele bir konumdan modelleme başlatılır ve gene rastgele adımlarla ilerlenir. $\pi$ sayısının hesaplanmasında olduğu gibi çok yavaş bir şekilde sonuca gitmek yerine, yeni atılacak adımların önem derecesini saptayarak daha akıllı bir istatiksel yaklaşım kurulur. Bunu yapabilmek için de önemi tanımlayan bir fonksiyon gerekir. Eğer çok büyük bir molekülün/moleküllerin yapısını bulmak istiyorsanız Boltzman dağılımı bu iş için biçilmiş kaftandır. Boltzmann dağılımı, bir sistemin belli bir durumda bulunma olasılığını gösterir. Bu olasılık ortamın sıcaklığı ve sistemin enerjisine göre belirlenir. Enerjisi düştükçe molekül daha kararlı olacağı için, yeni adımlarınızı enerjiyi düşürecek şekilde belirleyebilirsiniz. Tabii sıcaklığın etkisi nedeni ile bazen molekülünüz daha az kararlı hallere de kaçabilecektir. Bu koşullar altında başlangıç konumunuzu yavaş yavaş molekülün denge haline kadar götürebilirsiniz.
Günümüzün popüler konusu olan yapay zekâ/makine öğrenmesi gibi teknikleri de uygulayarak simülasyonda hem akıllı hem de rastgele bir yürüyüş yolu bulabilirsiniz.
Monte Carlo yöntemi uygulaması çok kolay bir modellemedir ve sadece bir rastgele sayı üretecine ihtiyacınız vardır.
Ersin Yurtsever
Bilim Akademisi üyesi
Koç Üniversitesi Kimya Bölümü öğretim üyesi