Bilişim Sistemi Nedir?
Bir bilişim sistemi belli bir konuya ya da örgüte ilişkin verileri bir düzen içinde sayısal ortamda saklayan ve kullanıcı ve başka sistemlerle etkileşim içinde bu veriler üzerinde arama bulma, değerlendirme, karar verme, çıkarsama işlemleri yapabilen bir sistemdir.
Bir bilişim sisteminin geliştirilmesinde harcanan zamanın ve emeğin büyük bir kısmı bilgisayar programlarında hata aramak, saptamak ve düzeltmekle geçer. Yazılım sistemleri geliştirildikten ve hatalardan makul ölçüde arındırıldıktan sonra gerçek kullanıma açılır. Uygulamaya geçtikten sonra ortaya çıkan hatalar ise sistem çalışırken ortaya çıktıkça sistem güncellemeleriyle birer birer onarılır. Nitekim kullandığımız çoğu bilgisayar işletim sistemindeki düzenli güncellemelerin amaçlarından biri de budur.
Yazılımın Doğruluğunun Kritik Sistemlerde Önemi
Kimi bilişim sistemlerinde en ufak yazılım hatasının bile sonuçları maliyet ve kullanıcıların güvenliği açısından vahim olabilir. Üstelik sistem, güncellemeler yapılmasına uygun değilse bu hataların düzeltilmesi de sistemi baştan kurmadan mümkün olmayabilir. Bu tür kritik sistemler, giderek artan oranlarda otomotiv, uçak, uzay, tren, hastane ve sağlık teknolojilerinde kullanılıyor.
Günümüzde uçak ve otomobillerin otomatik kontrol ve karar sistemleri ile aygıtlar arasındaki iletişim yazılıma dayanır. Bu yazılımlarda ortaya çıkabilecek en ufak bir hata bile sistemin düzgün çalışmasını ve yolcuların güvenliğini ciddi şekilde tehdit edebilir. Somut bir örnek vermek gerekirse, 2010 yılında Toyota Prius modellerde ortaya çıkan bir yazılım hatası zaman zaman, kısa bir süre fren pedalını etkisiz hale getiriyordu. Bunun üzerine şirket çok sayıda otomobili fabrikaya geri çağırmak zorunda kalmış, prestij kaybının yanında bu sürecin şirkete yol açtığı maddi zararların maliyeti 2 milyar dolar olarak bildirilmişti.
Sürücü güdümündeki klasik otomobillerin bile yazılımları hata içerebiliyor ve sorunlara yol açabiliyorsa, bugün birçok şirketin piyasaya sürmek üzere yarıştığı sürücüsüz taşıtlar için dile getirilen güvenlik ve güvenilirlik kaygıları da anlaşılabilir. Otonom taşıtların çok daha karmaşık olan yazılım sistemlerinin doğruluğunun saptanması bu alanda aşılması gereken en önemli engeldir.
Başka bir yazılım kazasına örnek vermek gerekirse, 1996 yılında 1 milyar dolar maliyetindeki Ariane 5 füzesi fırlatıldıktan kısa süre sonra bir yazılım hatası yüzünden kendini patlattı. Kritik yazılımlarda buna benzer hatalar ne yazık ki hâlâ bulunabiliyor: birkaç yıl önce Boeing 787 uçaklarında Ariana 5’tekine çok benzer bir yazılım hatası keşfedildi. Bu hata sadece uçağın bilgisayar sistemi 248 gün boyunca açık kalınca ortaya çıkıyor, ve tüm elektronik sistemin kapanmasına yol açıyordu.
Peki kritik bir bilişim sisteminin hatasız olduğundan emin olmanın ve var olan hataları sistematik bir şekilde saptamanın yolu ne olabilir?
Bu yazıda hata aramanın ve programların doğruluğunu kanıtlamanın genel bir yöntemini ele alarak bu soruya yanıt vereceğiz.
Burada tanıtacağımız yaklaşım, günümüzde sanayide çok sık kullanılan yöntemlerin temelini oluşturuyor. Birkaç örnek vermek gerekirse, yeni nesil Boeing ve Airbus uçaklarındaki tüm kritik programlar mutlaka bu yaklaşımla doğrulanıyor; öte yandan elektronik donanım sanayinde, üretilen karmaşık tüm devrelerin tasarımları da benzer şekilde hatalardan arındırılıyor. Bu yöntemler günümüzde kritik olmayan alanlarda bile kullanılıyor; örneğin Facebook birkaç yıldır kendi ürettiği tüm yazılımları bu tür yöntemlerle denetliyor.
Kritik Sistemlerde Test
Kritik bilişim sistemleri geliştirilirken muhakkak ki yazılım mühendisleri tarafından kapsamlı bir şekilde test edilir, ancak bu yeterli olmayabilir. Doğrulama sorununu açıklamak için aşağıdaki bilgisayar programını ele alalım. Program, girdi olarak $a,b$ tamsayılarını alıp, $c$ değerini $1/|a-b|$ sayısı olarak tanımlıyor.

Bu programın çok kritik bir projenin yazılımının içinde kullanılacağını düşünelim.
Yazılım test mühendisleri ele alınan bir programı çok sayıda farklı girdilerle çalıştırıp davranışını sınarlar. Bu program için aynısını yapalım.
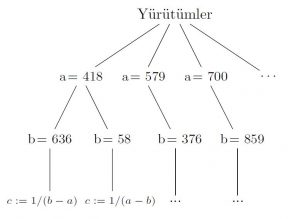
a ve b tamsayılarının $[0,2^{32}]$ aralığı içinden değer aldığını varsayalım. $2^{32}$ aşağı yukarı 4 milyar ediyor. Her girdi seçimi ve bu girdiler için programın gerçekleştirdiği işlemler dizisine yürütüm denir. Bu program her (a,b) girdi çifti için farklı bir yürütüm izler.
Farklı yürütümler elde etmek için rastgele a,b girdileri üretelim:
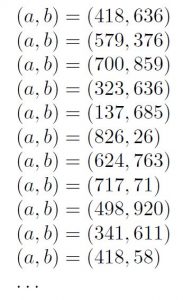
Bu girdilerden binlerce veya daha fazla üretebiliriz. Peki bu girdiler, ele aldığımız ufacık programı test etmek için yeterli olacak mıdır? Programlama bilenler bu programı diledikleri bir dilde yazıp rastgele üretilen değerlerle çalıştırabilirler.
Bu programda bir hata görüyor musunuz?
Burada deneyimli bilgisayarcılar ve matematikçilerin bile bazen dikkatsizlikle gözden kaçırabildiği bir hata şudur: Bölme işlemi bölen 0 olduğu zaman tanımsızdır ve hataya yol açar. Yani eğer $a=b$ ise, o zaman $\frac{1}{a-b} = \frac{1}{0}$ elde ederiz ki program burada hata verip kapanacaktır. Sıfıra bölme hatası içeren bir yürütüme hatalı yürütüm diyelim.
Sınadığımız yürütümlerin bazılarını aşağıdaki ağaç üzerinde temsil edelim.
Seçtiğimiz tüm yürütümleri temsil etmek fazla yer gerektireceğinden burada sadece birkaçını gösteriyoruz. Peki programın doğru çalıştığından emin olmak için kaç farklı yürütüme bakmamız gerekiyor? Her iki a,b tamsayısı da $2^{32}$ yani yaklaşık 4 milyar farklı değer alabildiğine göre $2^{32} \times 2^{32} = 2^{64}$ kadar farklı yürütüm var. Yani $10^{20}$’den bile fazla! Bu kadar yürütümün hepsine bakmak 3GHz hızındaki bir işlemciyle bile en az 500 yıl sürer!
Bir seçenek olarak tüm olası sayı çiftlerine bakmadan, kalite kontroldeki rasgele örneklemeye benzer şekilde çok sayıda rasgele test yapalım. Örneğin bir milyon rasgele girdi üretirsek, yukarıdaki hatayı bulma olasılığımız nedir?
Tek seferde $a=b$ tutturma olasılığı $1/2^{32}$ olduğuna göre, 1 milyon kere art arda başarısız olma olasılığı $$(1-\frac{1}{2^{32}})^{1000000} \approx 0.99$$
Yani rastgele bir milyon yürütüm denediğimizde çok büyük olasılıkla bu hatayı gözden kaçıracağız.
Bunun sebebi kabaca şöyle görülebilir. Girdi değerlerini $2^{32}\times2^{32}$ boyutlu bir matris olarak görürsek, hata sadece $2^{32}$ boyutlu köşegen elemanları için ortaya çıkıyor. Yani kabaca dört milyar denemenin sadece birinde bu hata ortaya çıkar. Burada neredeyse kesin biçimde $a=b$ durumuna rastlamak için tam olarak kaç kez test yapılması gerektiği hesabını okurlara bırakıyoruz.
Peki hatayı oluşturan koşulu önceden bilmiyorsak ne kadar rasgele test yapmamız gerektiğini nasıl bileceğiz? Ya da iki değil, çok sayıda girdi varsa, bu işin içinden nasıl çıkacağız?
Yazının devamında bu tür “dertlere” çözüm olarak kaba kuvvet testler yerine formel doğrulamanın nasıl yapıldığını anlatacağız.
Soyutlama ile Doğrulama
Problemi soyutlayarak doğrulamayı nasıl kolaylaştıracağımızı ve her olası şıkkı kapsayacağımızı yukarıdaki çok basit bölme problemine uygulayarak gösterelim. Eğer amacımız programın sıfıra bölmediğini göstermek ise aslında tüm yürütümleri denemenin bir anlamı yoktur. Sadece $a=b$ eşitliğini sağlayan girdilerle denemek yeterli çünkü programda bölen olarak yer alan ifadeler sadece $a-b$ ve $b-a$, ve her ikisi de ancak $a=b$ koşuluyla sıfırlanır.
Girdileri ayrı ayrı normal tamsayılar olarak görmek yerine a,b girdi ikilisini bir soyut girdi olarak ele alalım. Soyut girdiler şu üç değeri alabilsin:
$$D_{a < b},~~ D_{a=b},~~ D_{a>b}$$
Bu sayede yapmak istediğimiz bir tek soyut değer ile gelişigüzel büyüklükteki girdi ikilileri kümesini temsil edebilmek. Örneğin $D_{a<b}$ değeri aslında $a<b$ eşitsizliğini sağlayan tüm girdi ikililerini temsil ediyor.
Amacımız $a<b$’yi sağlayan tüm girdileri denemek yerine bunları tek bir soyut değer ile hep birden ele almak.
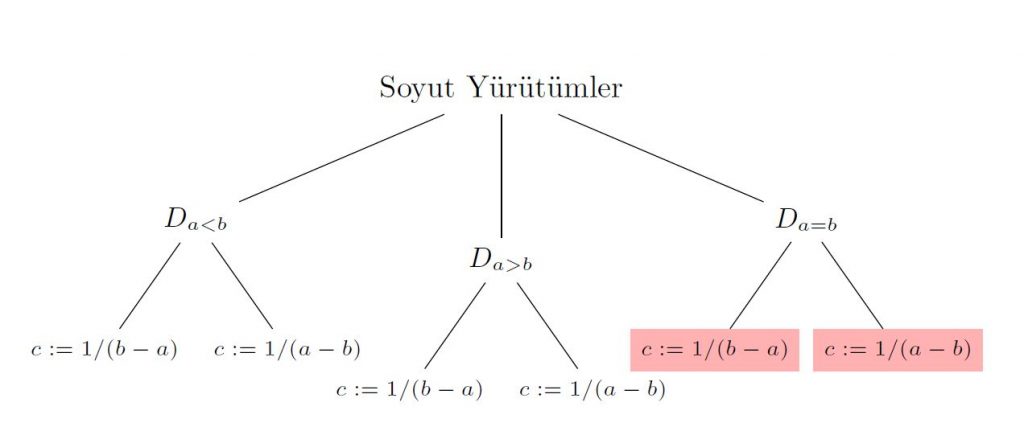
Her soyut girdi seçimi ve bu soyut girdiler için programın gerçekleştirdiği işlemler dizisine soyut yürütüm diyelim. Yukarıda nasıl yürütüm ağacını oluşturduysak, soyut girdiler ile soyut yürütüm ağacını oluşturabiliriz. İşimizi kolaylaştırmak için programın ilk iki satırını tek bir işlem gibi düşünelim ve aşağıdaki soyut girdiler ağacını bu şekilde oluşturalım.
En soldaki soyut yürütümü inceleyelim. İlk satırda okunan $a,b$ değerlerinin $a<b$ koşulunu sağladığını varsaydık. Ardından $D_{a<b}$ soyut girdisi sayesinde eğer-değilse ifadesinin koşulunun doğru olduğunu belirleyip ilk dalındaki işlemi gerçekleştirdik.
Ağaçtaki ikinci yürütümde simetrik şekilde $D_{b<a}$ soyut girdisi ile yürütümün ikinci dalını gerçekleştirdik. Üçüncü dalda ise $D_{a=b}$ soyut girdisi ile yine ikinci dalı gerçekleştirdik. Ancak bu sefer, $1/(a-b)$ ifadesinin sıfıra bölme olduğunu soyut girdinin belirlediği $a=b$ eşitliği sayesinde saptadık. Hatayı sadece üç yürütüme bakarak buluverdik.
Karmaşık İfadeli Programlar
Peki yukarıdaki soyut girdi yöntemi herhangi bir problem, her tür program için de geçerli midir?
Yukarıdaki örnekte eğer-değilse ifadesinde bulunan $a<b$ koşulunu soyut girdiler arasında seçerek, soyut yürütümlerde bu koşulun doğruluğunun saptanmasını mümkün kıldık.
Ancak eğer-değilse ifadesi, aşağıdaki gibi daha karmaşık başka bir koşul içeriyor olsaydı ne yapacaktık?
Önce bu programı ele alalım.

Ele aldığımız soyut girdiler sadece $a=b, a<b, a>b$ ilişkilerini belirlediğinden buradaki $a*a-b*b > 15*a+b$ koşulunun doğruluğunu karmaşık hesaplar yapmadan belirlemek mümkün değil.
Bu hesabı yapamayacağımızı varsayarsak, soyut yürütüm ağacı şu kural uygulayarak oluşturulur. Doğruluğunu belirleyemediğimiz ifadelerin hem doğru hem yanlış olabileceği varsayılır. Örneğin burada, $a<b$ koşulunu sağlayan girdiler için programın eğer-değilse ifadesinin her iki dalından da geçebileceğini varsayıyoruz. Tabii, gerçekte her $a,b$ girdisi için yürütüm ya birinci dalı ya da ikinci dalı izleyecektir; hiçbir girdi için her iki dal birden izlenmez. Ancak, amacımız varolan tüm hataları bulmak olduğu için ne olur ne olmaz, gerçekte mümkün olmayan yürütümleri de ele alıyoruz.
Eğer bir soyut yürütüm a,b tamsayı değerleri seçilerek gerçek bir yürütüme dönüştürülebiliyorsa, ona gerçeklenebilir soyut yürütüm, hiçbir a,b değeri için gerçek bir yürütüme dönüştürülemiyorsa, yalancı soyut yürütüm denir. Gerçeklenebilir veya yalancı soyut yürütüm bir hata içeriyorsa ona hatalı soyut yürütüm denir.
Yukarıdaki ağaçtaki kimi soyut yürütümler gerçek kimisi is yalancıdır. Örneğin en soldaki $D_{a<b}; c := 1/(b-a)$ yürütümüne bakalım. Burada eğer-değilse ifadesinin doğru olduğu varsayılmış, demek ki, $a^2 – b^2 > 15*a + b$. Ancak $a,b\geq 0$ olduğu için bu $a^2 – b^2 > 0$ demek oluyor. Çarpanlarına ayırırsak $(a-b)(a+b) > 0$, yani $a-b<0$ olamaz. Diğer bir deyişle tam bu soyut yürütümü izleyen $a,b$ tamsayıları yoktur.
Hiçbir hatayı gözden kaçırmamak için önemli olan programdaki her hatalı yürütümün gerçeklenebilir ve hatalı bir soyut yürütüme denk gelmesi. Burada $a=b=0$ girdileri hatalı bir yürütümü tanımladığı gibi, $D_{a=b}$ soyut girdisiyle gerçeklenebilir ve hatalı soyut yürütüme de denk geliyor.
Özetlemek gerekirse, bu yöntem her program için uygulanabilir. Programdaki her hatalı yürütüm gerçeklenebilir ve hatalı bir soyut yürütüm olarak saptanacaktır: diğer bir deyişle bu yöntem kapsayıcı bir sınama yapmaya denk geliyor.
Eğer bu yöntem bir programda hata bulamıyorsa, o programda gerçekten hata yok demektir. Öte yandan, yukarıda da gördüğümüz gibi bu yöntemin bulduğu her hatalı soyut yürütüm gerçek bir hataya denk gelmiyor.
Demek ki bu yöntemin kullanıcısının bulunan hatalı soyut yürütümleri, gerçeklenebilir mi yoksa yalancı mı olduğunu belirlemek için teker teker incelemesi gerekiyor.
Soyutlamanın Zenginleştirilmesi
Eğer doğruluğunu belirleyemediğimiz çok sayıda eğer-değilse ifadesi varsa, soyut yürütüm sayısı artabilir; daha da önemlisi çok sayıda yalancı hatalı soyut yürütümler ortaya çıkabilir. Bu da kullanıcının çok sayıda soyut yürütümü denetleyeceği anlamına geldiğinden işini ciddi derecede zorlaştırabilir.
Aşağıdaki örnekte bu konuya değiniyoruz.
Bu sefer program son satırda sıfıra bölme hatası içeriyor. Ancak önceki satırlarda böyle bir hata yok: eğer-değilse ifadesinin birinci dalında $a-1>0$ olduğu belli, ikinci dalda ise bölen zaten her zaman pozitif.
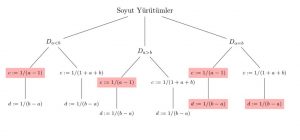
Yukarıda ele aldığımız soyut girdilerle aynı yöntemi uygularsak aşağıdaki soyut yürütüm ağacı ortaya çıkıyor.
Bu ağaçtaki hatalı soyut yürütümlerden biri şu: $D_{a<b}, c := 1/(a-1)$. Bunun sebebi, eğer-değilse ifadesinin $a>1$’in değeri $a<b$ koşulu ile belirlenemediğinden her iki dalın da mümkün varsayılması. Birinci dal içerisindeki bölme işlemi gerçekleştirilirken $a-1 = 0$ olup olmadığı da sırf $a<b$ bilgisiyle belirlenemediği için olası bir hata olarak saptanıyor.
Bir önceki örnekte gördüğümüz gibi, burada da gerçek bir hataya denk gelmeyen yalancı ve hatalı soyut yürütümler ortaya çıkıyor. Diğer bir deyişle bu soyut yürütümler hatalı göründüğü halde gerçek bir hataya denk gelmiyor.
Öte yandan bu yöntemi daha duyarlı hale getirmek, yani daha az yalancı hatalı soyut yürütüm bulmasını sağlamak mümkün.
Bu bölümün başında seçtiğimiz soyut girdiler kümesini zenginleştirebilir ve programa uygun hale getirebiliriz. Soyut girdiler kümesini $a>1$ koşulunu ekleyerek zenginleştirelim.
Yeni soyut girdiler kümesi:
$D_{a < b, a>1}, ~~D_{a=b,a>1}, ~~D_{a>b,a>1},~~ D_{a < b, a\leq 1},~~ D_{a=b, a\leq 1}, ~~D_{a>b, a\leq 1}$
Bu sefer eğer-değilse ifadesi $a>1$ bilgisi sayesinde belirlenebiliyor, ve yukarıdaki yürütüm dışlanıyor. Yöntemimiz doğru bir şekilde sadece son satırdaki hatayı buluyor. Yenilenen soyut yürütüm ağacı aşağıda.
Soyutlamanın seçilmesi
Genel bir kural olarak, incelemek istediğimiz bir programdaki eğer-değilse ve döngü koşullarının belirlenebileceği bir soyutlama seçmek bu yöntemin duyarlılığını arttırır. Bunu yapmanın en basit yolu, yukarıda yaptığımız gibi, bu ifadelerde yer alan koşulların hepsini soyut girdilere eklemek. Eğer bunların sayısı fazla ise koşullar teker teker, yalancı hata buldukça da eklenebilir.
Soyutlama ve Program Doğrulama
Bu yazıda açıkladığımız soyutlama yöntemi program doğrulamada en sık kullanılan yöntemlerden biridir. Program soyutlamanın kuramı, soyut yorumlama (abstract interpretation) adı altında ilk kez 1977’de Fransa’da yayımlanmış ve geliştirilmiş, bu sayede Airbus’ın A380 uçağının C dilindeki kontrol yazılımı tamamen doğrulanmıştır. Bunun dışında günümüzde sanayide düzenli olarak kullanılan yöntemlerden biridir.
Soyut yorumlama dışında çok sayıda doğrulama yöntemi vardır. Bunlar uygulandığı sistemlerin türüne göre kullanılır. Örneğin yazılım, kontrol sistemleri, donanım, gerçek zamanlı sistemler birbirinden çok farklı özellikler ve doğrulama gereksinimleri içerir.
Daha fazla bilgi için İngilizce birkaç anahtar sözcük: formal verification, abstract interpretation, model checking, model-based testing, symbolic execution
Ocan Sankur
Fransız Ulusal Bilimsel Araştırma Merkezi (CNRS)