2024 Nobel Fizik Ödülü makine öğrenmesi alanında çığır açan çalışmalara verildi. Bu ödül, makine öğrenmesinin temellerini fizik prensiplerini kullanarak atan Hopfield Ağları[1]Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences, 79(8), 2554-2558. ve Boltzmann Makineleri[2]Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive science, 9(1), 147-169. üzerindeki araştırmaların önemini bir kez daha vurguladı.
Makine öğrenmesi, yalnızca mühendislik ve veri bilimi değil, aynı zamanda fizik ve biyoloji gibi temel bilimlerde de geniş bir uygulama yelpazesine sahip. Örneğin, fizik alanında parçacık fiziği verilerinin analizi[3]Radovic, A., Williams, M., Rousseau, D., Kagan, M., Bonacorsi, D., Himmel, A., … & Wongjirad, T. (2018). Machine learning at the energy and intensity frontiers of particle physics. Nature, 560(7716), 41-48., biyolojide gen dizilimleri üzerinde yapılan çalışmalar[4]Eraslan, G., Avsec, Ž., Gagneur, J., & Theis, F. J. (2019). Deep learning: new computational modelling techniques for genomics. Nature Reviews Genetics, 20(7), 389-403. ve sağlık alanında hastalıkların erken teşhisi[5]Esteva, A., Robicquet, A., Ramsundar, B., Kuleshov, V., DePristo, M., Chou, K., … & Dean, J. (2019). A guide to deep learning in healthcare. Nature medicine, 25(1), 24-29. gibi birçok yenilikçi uygulamadan bahsedebiliriz. Hatta bu yılki Nobel Kimya Ödülü de yapay zekâ kullanarak karmaşık protein yapılarını tahmin etme ve tasarlama çalışmalarıyla biyolojik araştırmalarda devrim yaratan David Baker, Demis Hassabis ve John Jumper’a verildi. Bu bilimsel etkilerin dışında makine öğrenmesi, endüstride de örneğin otomotiv sektöründe otonom sürüş ve finans sektöründe risk analizi gibi alanlarda da etkin olarak kullanılıyor. Tüm bu gelişmeler, 1980’lerde John J. Hopfield ve Geoffrey E. Hinton’un istatistiksel fiziği temel alan yöntemleri ile mümkün hale gelmiştir.
Makine öğrenmesinin tarihine göz atıldığında, ilk dönemlerde temel hedeflerin başında veri analizi ve örüntü tanıma yer alıyordu. Hopfield’ın geliştirdiği Hopfield Ağları, bellek modelleme konusunda devrim yaratarak, yapay sinir ağları içerisinde yeni bir paradigmanın temelini attı. Bu ağlar, enerji minimizasyonu ve spin cam teorisi gibi termodinamik ilkeleri kullanarak örüntü tanıma sağlarken, deterministik bir süreçle çalışır. Öte yandan Hinton’un Boltzmann Makineleri, Hopfield ağlarını stokastik süreçlerle birleştirerek öğrenme sürecini derinleştirmiştir. Dolayısıyla, bu iki model, makine öğrenmesinin temel yapı taşlarını oluşturmakla kalmaz, aynı zamanda fizik gibi geleneksel disiplinlerin sınırlarını zorlayarak birçok alanda önemli bilimsel atılımların kapısını aralamış olur.
Bu yazıda istatistik fiziğin karmaşık sistemlerin anlaşılması için ortaya koyduğu yaklaşımlara değindikten sonra Hopfield ve Hinton’un çalışmalarını kısaca anlatacağız. Son bölümde ise 2024 Nobel Fizik Ödülü’nün doğrudan bir fizik problemi yerine makine öğrenmesi gibi disiplinlerarası bir alana verilmesi konusundaki tartışmalara yer vereceğiz.
İstatistiksel fizik nedir? Dinamik sistemler nasıl modellenir?
İstatistiksel fizik, çok parçacıklı sistemlerin davranışlarını anlamak ve açıklamak için istatistiksel yöntemler kullanan bir fizik dalıdır. Tek tek parçacıklara odaklanmak yerine, araştırmacılar çok sayıda parçacığın toplu davranışına bakar. Bu, sistemin büyük ölçekte ortaya çıkan özelliklerini – sıcaklık, basınç, manyetizma gibi – anlamalarına yardımcı olur. Örneğin Ernst Ising, 1920’lerde manyetizma için bir model geliştirmiştir.
Ising modelinde bir örgü boyunca dizilmiş atomlar bulunduğu düşünülür, her atomun +1 veya -1 olmak üzere bir spini vardır ve bu atomlar spinleri dolayısıyla birbiriyle etkileşmektedir. Ising modeli, bu ağdaki her atomun komşularıyla etkileşime girerek, düşük enerji durumuna yönelme eğiliminde olduğunu gösterir.
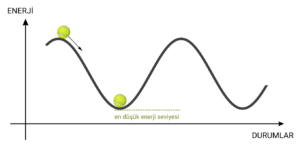
Dinamik sistemlerin düşük enerji durumuna yönelme eğilimi, bir platform üzerindeki küre örneğiyle basitçe tasvir edilebilir. Bu analojide, küre belirli bir yükseklikten serbest bırakıldığında yerçekimi etkisiyle en düşük enerji seviyesine, yani platformun en alçak noktasına doğru hareket eder.
“En düşük enerji seviyesi” fiziksel sistemlerde enerji minimizasyonu ilkesine dayanır; bu, sistemin daha kararlı bir duruma ulaşmasını sağlar. Kararlı durumlardaki sistemler, yani örneğin görseldeki top en düşük enerji seviyesindeyken, küçük değişikliklerden sonra yeniden aynı noktaya dönme eğilimindedir. Dinamik sistemler, dış kuvvetler olmadan kendilerini denge noktasına yönlendiren kuvvetlerin etkisi altındadır.
Ising, manyetizmayı, basitleştirilmiş ağ modelindeki atomların spinlerinin komşularıyla etkileşerek kollektif bir davranış sergilemesi olarak ele almıştır.
Hopfield ağları: İstatistiksel fizik ile örüntü tanıma

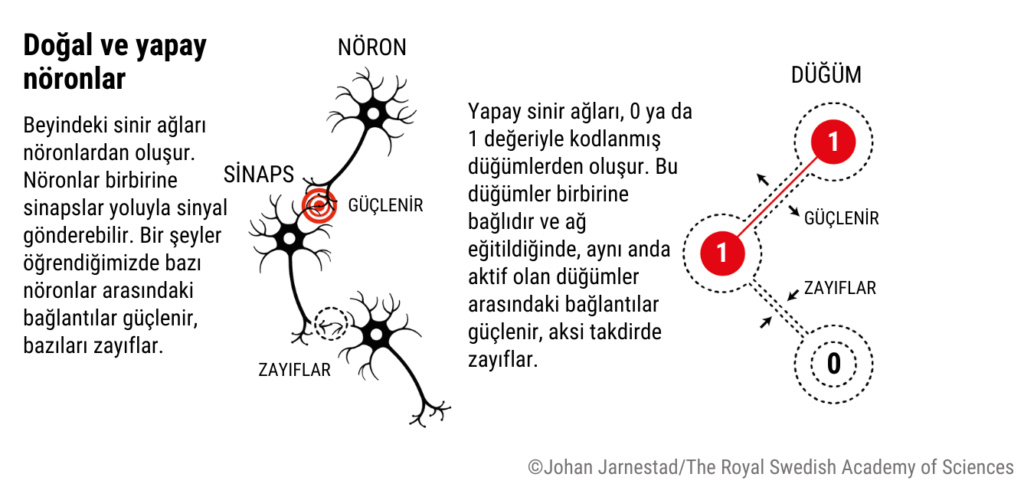
John J. Hopfield, 1982’de geliştirdiği Hopfield Ağları ile bellek modellemede istatistiksel fiziğin kavramlarını yapay sinir ağlarına entegre etti. Bu modelde, beyindeki sinirlerin etkileşimi ile durum değiştirmeleri, Ising modeli gibi fiziksel sistemlerdeki benzer etkileşimlerle ilişkilendirilmişti. Beyindeki nöronlar da, Ising modeline benzer şekilde, bir etkileşim ağı oluşturur ve bir uyarıcıya yanıt olarak sinirsel durumlarını değiştirir. Hem beyindeki sinir ağları hem de Ising modeli, komşu etkileşimlerinin sistemin genel durumunu yönlendirdiği enerji minimizasyonu veya dengeye ulaşma süreçlerine dayanır. Bu dinamik sistemlerde, bireysel elemanların davranışları (nöronlar veya spinler) tüm sistemin genel davranışını belirler.
Hopfield Ağları’nda her nöron, diğer tüm nöronlarla etkileşim içinde bulunarak yinelemeli bir yapı oluşturur. Yapay sinir ağlarında “bellek,” ağın öğrenme sürecinde tanıyabileceği, hatırlayabileceği veya yeniden oluşturabileceği desenler veya durumları ifade eder. Beyin veya bir hesaplama sisteminde bellek, bilginin kodlanması, depolanması ve geri çağrılması süreçleri olarak tanımlanırken, Hopfield Ağları bu süreçlerin yapay ortamda modellenmesine olanak tanır.
Bir yapay sinir ağını eğitmek, bu platformu istenilen şekilde tasarlamak gibidir. Platform üzerindeki her çukur, sisteme eklenen bir bellek desenini temsil eder. Küre, çukura yakın bir noktadan bırakıldığında, enerji minimizasyonu ilkesi doğrultusunda o bellek desenine ulaşır. Yapay sinir ağlarındaki bellekler de tıpkı fiziksel dünyada olduğu gibi, minimum enerji seviyesine ulaşmaya eğilimlidir. Bu yöntem, birden fazla bellek deseninin aynı ağda etkili bir şekilde saklanmasını ve aranmasını mümkün kılar.
Hopfield Ağı dinamikleri, fizik dünyasından gelen Ising modeli ile benzerlik gösteren bir enerji fonksiyonu ile tanımlanır.
$$E=-\frac{1}{2} \Sigma_{i,j} w_{ij} s_i s_j – \Sigma_i h_i s_i$$
Burada $E$ toplam enerji, $w_{ij}$ nöronlar arası bağlantı ağırlıkları, $s_i$ nöron durumları (sadece -1 veya +1 olarak temsil edilir ve Ising modelindeki spinlere benzemektedir) ve $s_i$ nöronlara uygulanan yanılma (bias) terimidir (Ising modeldeki dış manyetik alana benzemektedir).
Hopfield ağı, girdiyi (yukarıdaki örnekte kürenin bırakıldığı noktayı) işlerken enerjiyi minimize ederek en düşük enerji durumuna ulaşmayı amaçlayan deterministik bir süreçle çalışır. Bu süreç, Ising modelindeki parçacıkların etkileşim yoluyla kararlı bir enerji durumuna ulaşmasına ve bellek geri çağırma işleminin fiziksel sistemlerin enerji minimizasyonu yoluyla en düşük yapılandırmalara ulaşmasına benzer. Ağ, nöron durumlarını yineleyerek, eksik veya gürültülü veriler içerse bile daha önce kaydedilmiş anıları hatırlama yeteneğine sahiptir. Hopfield Ağları, bu mekanizma sayesinde örüntü tanıma ve bellek simülasyonu alanında çığır açan bir yöntem olarak kabul edilmektedir.
Boltzmann Makineleri: Termodinamik ve stokastik öğrenme

Geoffrey Hinton, 1985’te Boltzmann Makineleri’ni geliştirerek enerji minimizasyonu ilkesini daha ileri bir boyuta taşımıştır. Hopfield Ağları kayıtlı anıları geri çağırırken, Boltzmann Makineleri doğrudan veriden örüntüleri öğrenir ve yeni örüntüler oluşturur. Boltzmann Makineleri, Boltzmann dağılımına göre hesaplanan bir stokastik davranış sergiler.
$$P(s) \propto e^{-\beta E(s)}$$
Burada $P(s)$ belirli bir durumun olasılığı ve $\beta$ sıcaklık parametresidir.
Boltzmann Makineleri, termodinamikten ilham alarak stokastik bir yapı sunar. Enerji fonksiyonu Hopfield Ağlarındaki denklemin aynısı olmasına rağmen, nöronlar rastgele olarak $P(s)$ dağılımına göre farklı bir enerji seviyesi seçebilirler. Bu stokastik davranış, nöronların yüksek enerjili durumlarda bulunmasına olanak tanıyarak ağın daha genel bir çözüm bulmasını sağlar. Örneğin, yukarıdaki küre analojisini kullanacak olursak, Boltzmann Makineleri, kürenin yalnızca yerel bir çukurda kalmasını engelleyerek, kürenin platform üzerindeki daha derin bir çukura ulaşmasını sağlar. Bu sayede, Boltzmann Makineleri, verinin yerel minimumlara saplanmadan daha güçlü örüntüleri öğrenmesine olanak tanır.
Hinton’un bu yeniliği, makine öğrenmesinde termodinamik kökenli bir modelin geliştirilmesine olanak tanımış ve günümüz derin öğrenme yöntemlerinin temelini atmıştır. Boltzmann Makineleri, birçok derin öğrenme modelinin temelini oluşturan enerji tabanlı yaklaşımların ilk örneklerinden biridir ve yapay zekâ alanında önemli bir yere sahiptir.
Paul Smolensky 1986’da Boltzmann Makinelerine gizli nöronlar ekleyerek Kısıtlı Boltzmann Makinelerini ortaya atmış ve öğrenme sürecini derinleştirmiştir.[6]Smolensky, P. (1986). Information processing in dynamical systems: Foundations of harmony theory. Bu, birçok derin öğrenme modelinin temelini oluşturan enerji tabanlı yaklaşımların ilk örneklerinden biridir. Gizli katmanlar, verinin karmaşıklığını daha iyi temsil etmeye ve öğrenme yeteneğini artırmaya yardımcı olarak, yapay zekâ alanında önemli bir yere sahiptir.
Nobel Ödülü: Disiplinlerarası araştırma ve fiziğin sınırları
2024 Nobel Fizik Ödülü, doğrudan fizik problemlerine değil, makine öğrenmesi gibi disiplinlerarası bir alana verilmesi nedeniyle tartışmalara yol açtı. Bu durum, bilimsel ödüllerin neye göre verileceği ve hangi kriterlerin dikkate alınması gerektiği konusunda önemli bir sorgulamaya neden oldu. 2024 Nobel Fizik Ödülü, belirli bir disiplindeki başarıların yanı sıra, bu başarıların diğer alanlarla olan ilişkilerini ve etkilerini de yansıtma potansiyeline sahip olduğunu gösterdi.
Hopfield Ağları ve Boltzmann Makineleri’nin geliştirilmesi, istatistiksel fizik, karmaşık sistemler ve sinir ağları arasındaki köprüyü kurarak makine öğrenmesinin araştırma alanındaki yerini güçlendirmiştir. Ödüllerin belirli bir çalışmaya verilmesi, kişilere veya onların yaşamları boyunca yaptıkları işlerin tümüne değil, belirli bir katkıya odaklanması anlamına gelir.
Bu bağlamda, makine öğrenmesi gibi yenilikçi yaklaşımlar, fiziksel dünyanın karmaşık yapılarından ilham alarak önemli bilimsel atılımlar sağlar. Ayrıca, istatistiksel fizik ve makine öğrenmesi arasındaki kesişim, fiziksel ilkelerin yapay zeka sistemlerini geliştirmede nasıl kullanılabileceğini göstermektedir. On yıl önce, bu tür bir tanınmanın olası olmadığı düşünülüyordu. Ancak günümüzde, teorik ve hesaplamalı fizik arasındaki bu yaklaşımlar, disiplinlerarası araştırmanın önemini vurgulayarak bilimin sürekli evrimi içinde yeni paradigmaların ortaya çıkmasına olanak tanımaktadır.
Sonuç olarak, 2024 Nobel Fizik Ödülü’nün makine öğrenmesi alanındaki çalışmalara verilmesi, araştırma alanında önemli bir dönüm noktasını temsil ediyor. Makine öğrenmesi, istatistiksel fizik ile birleşerek, geleneksel bilimsel disiplinlerin sınırlarını zorlamakta ve yeni araştırma alanları açmaktadır. Bu çok disiplinli etkileşimler, gelecekte daha fazla yenilikçi çözüm ve teknolojinin ortaya çıkmasına zemin hazırlayacaktır.
“Nobel Fizik Ödülü bir fizik araştırmasına mı verilmeli, yoksa çığır açabilecek disiplinlerarası çalışmalara da gidebilmeli mi?” sorusunun cevabını yorumsuz olarak okuyuculara bırakıyoruz.
Deniz Eroğlu (Kadir Has Üniversitesi, Mühendislik ve Doğa Bilimleri Fakültesi)
Uğur Tırnaklı (Bilim Akademisi üyesi, İzmir Ekonomi Üniversitesi, Fizik Bölümü)
Notlar/Kaynaklar
| ↑1 | Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences, 79(8), 2554-2558. |
|---|---|
| ↑2 | Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive science, 9(1), 147-169. |
| ↑3 | Radovic, A., Williams, M., Rousseau, D., Kagan, M., Bonacorsi, D., Himmel, A., … & Wongjirad, T. (2018). Machine learning at the energy and intensity frontiers of particle physics. Nature, 560(7716), 41-48. |
| ↑4 | Eraslan, G., Avsec, Ž., Gagneur, J., & Theis, F. J. (2019). Deep learning: new computational modelling techniques for genomics. Nature Reviews Genetics, 20(7), 389-403. |
| ↑5 | Esteva, A., Robicquet, A., Ramsundar, B., Kuleshov, V., DePristo, M., Chou, K., … & Dean, J. (2019). A guide to deep learning in healthcare. Nature medicine, 25(1), 24-29. |
| ↑6 | Smolensky, P. (1986). Information processing in dynamical systems: Foundations of harmony theory. |