Bugünlerde herkes yapay zekâdan bahsediyor. Gelecek yapay zekâda deniyor, çağımızın elektriği benzetmesi yapılıyor, yapay zekâ üstüne yeni şirketler kuruluyor, eski şirketler yapay zekâya geçmenin faydalarını anlatıyor. Buna ön ayak olan bilim insanları sürekli haberlerde yer alıyor, ki buna en son örnek bilgisayar bilimlerinin en önemli ödüllerinden biri olan Turing ödülünün bu konuda çalışan üç kişiye, Yoshua Bengio, Geoffrey Hinton ve Yann LeCun’e verilmesi oldu. Bu yazıda bu konuda yapılmış çalışmaları kısaca özetleyip konunun kendimce önemli yanlarını anlatacağım.
Yapay Öğrenme
Bu son yıllarda yapay zekâ derken kast ettiğimiz aslında yapay öğrenme. Bilgisayarları zeki yapmak için on yıllarca uğraştıktan sonra yakın zamanda bunun en iyi yolunun öğrenme olduğunu anladık. Bir dilden ötekine, örneğin İngilizceden Türkçeye çeviri için araştırmacılar on yıllarca kurallar çıkarmaya uğraştılar ama bu kuralların başarısı hep kısıtlı kaldı; artık yaptığımız böylesi kuralları insanların düşünüp programlaması yerine veriden öğrenmek. Yani çok büyük bir metin verisi toplayalım, içinde aynı cümleler her iki dilde de yazılmış olsun, ve bu cümle çiftleri arasında gereken eşleme kurallarını, öğrenen bir program kendisi veriden çıkarsın. Bu öğrenme yöntemleri içinde de son yıllarda en başarılı olanlar yapay sinir ağları ve bu sinir ağlarının büyük olanlarına da derin ağ diyoruz.
Böylesi sinir ağlarının ve derin öğrenmenin ne olduğunu anlamak için en basit model olan doğrusal modelle başlayalım:
$$y=w_0+w_1 x_1 +w_2 x_2~~~~~~~~~~~~~~ (1)$$
Burada $x_1$ ve $x_2$ ile gösterdiğimiz iki tane girdi var, $y$ ise çıktıyı gösteriyor. Başka uygulamalarda girdi yüzlerce, binlerce olabilir, burada iki girdi varsaydım; çıktı da burada bir tane ama daha çok da olabilir. $w_0, w_1, w_2$ ise modelin parametreleri. Bu genel modeli, $w_0, w_1$ ve $w_2$ ağırlıklarını değiştirerek istediğimiz uygulamaya uyarlayabiliriz. Öğrenmeyle kast ettiğimiz de bu: Varsayılan modelin parametrelerini veriye bağlı olarak ayarlayarak genel modeli belli bir iş için özelleştirmek.
Örneğin ikinci el araba fiyatını tahmin etmek istediğimizi düşünelim. Girdi arabanın özellikleri, çıktı da fiyatı olacak. Bu yapay öğrenme için iyi bir örnek uygulama, çünkü bu algoritmasını bilmediğimiz bir iş. Arabanın fiyatını etkileyecek birçok özellik olabilir ama $x_1$ olarak arabanın motor gücünü, $x_2$ olarak ise arabanın kaç kilometre yapmış olduğunu kullandığımızı varsayalım. Çıktı $y$ ise arabanın fiyatını, örneğin sıfır kilometre fiyatının yüzde kaçı ettiğini göstersin. Burada en basit model olarak yukarıda (1)’de yazdığımız doğrusal modeli kullanabiliriz. Piyasada bir araştırma yapıp yakın zamanda satılmış $N$ tane arabanın motor gücü, kilometre, ve fiyatlarını ($x_1^t, x_2^t, y^t$), $t=1, …, N$ üçlüleri biçiminde toplayıp bu veri üstünde en doğru tahmini yapmamızı sağlayacak $w_0, w_1$ ve $w_2$ değerlerini kare hatayı en küçük yapacak biçimde bulabiliriz. Bu istatistikte doğrusal regresyon denilen çok eski, Gauss’tan beri bilinen bir yöntem.
Denklem (1)’deki doğrusal model her ne kadar basit ve güzelse de her zaman iyi bir model olmayabilir. Kullanılmış araba fiyatında örneğin arabanın kaç kilometre yaptığının etkisi hep aynı değildir; 2.000 km’den 3.000 km’ye geçerkenki fiyat farkı, 20.000 km’den 21.000 km’ye göre daha çoktur, dolayısıyla geniş bir $x_2$ aralığındaysak sabit bir $w_2$ varsaymak doğru olmaz.
Doğrusal modelin yeterli olmadığı durumda modelin karmaşıklığını arttırmak gerekir. Örneğin ikinci dereceden bir model kullanılabilir:
$$y=w_0+w_1 x_1+w_2 x_2+w_3 x_1 x_2 + w_4 x_1^2 +w_5 x_2^2 $$
Bu model doğrusal modele göre daha esnek, dolayısıyla kullanım alanı daha geniştir. Ağırlıkları yine aynı biçimde öğrenebiliriz, çünkü
$$z_1=x_1,~~ z_2=x_2,~~ z_3=x_1 x_2, ~~z_4=x_1^2, ~~z_5=x_2^2$$
diye yeniden tanımlarsak bu modeli şöyle de yazabiliriz:
$$y=w_0 + w_1 z_1 +w_2 z_2+w_3 z_3+w_4 z_4 +w_5 z_5$$
Burada iki boyutlu $x$ uzayından beş boyutlu $z$ uzayına geçtik; $x$ uzayındaki ikinci derece model, $z$ uzayında doğrusal bir modele karşılık geliyor. Yani doğrusal olmayan bir ön işlemeden sonra doğrusal modelimizi kullanabiliyoruz.
İstersek ikiden daha yüksek derecelere de çıkabiliriz ama $x$’in kuvvetleri kullanabildiğimiz tek ön işleme değil; yeni $z$ değerlerini başka taban fonksiyonlarını kullanarak da hesaplayabiliriz, örneğin $z_1=\sin(x_1), z_2=\exp(-x_1^2/4)$, vs. Herhangi bir çıktıyı belli taban fonksiyonlarının ağırlıklı toplamı olarak yazmak hem istatistik, hem sinyal işlemede çok sık kullanılan bir yaklaşım, ve farklı uygulamalarda sık kullanılan farklı taban fonksiyonları var. Bir başka yapay öğrenme yöntemi olan destek vektör makinelerindeki çekirdek fonksiyonu da yine bu taban fonksiyonu düşüncesine dayanıyor; bu yaklaşımın en iyi yanı bir kez taban fonksiyonlarını sabitlediğimizde $w$ değerlerini öğrenmenin kolay olması.
Bir sonraki adım olarak, bir aşama daha ileri gidip yalnızca taban fonksiyonlarını nasıl birleştireceğimizi değil, taban fonksiyonlarının kendilerini de öğrenmek istediğimizi düşünelim. Yani bizim kare mi alsak, ya da sinüs mü kullansak diye herhangi bir karar vermemize gerek kalmadan yalnızca veriye bağlı olarak ne taban fonksiyonu gerekiyorsa onu öğrenebilir miyiz?
Amacımız taban fonksiyonunu genel bir model olarak yazıp onun parametrelerini de veriden öğrenmek. Bu durumda çıktıyı şöyle yazıyoruz:
$$y=w_0 +w_1 z_1+w_2 z_2 + ….+w_H z_H$$
$$=w_0+w_1 g(x_1, x_2 | v_1)+w_2 g(x_1, x_2 | v_2)+…+w_H g(x_1, x_2 | v_H)~~~~~~~~~~~~(2)$$
Burada $g(x_1, x_2 | v_i)$ ile gösterdiğimiz taban fonksiyonu; $g$ genel bir model, $v_i$ onun parametresi (çoğu zaman bir vektör) ve $v_i$’nin değerine göre $g$ özelleşiyor. Çıktıyı, $H$ tane böyle veriye uyarlanmış taban fonksiyonunun ağırlıklı toplamı olarak yazıyoruz. Yani öyle $H$ tane $g$ öğrenmek istiyoruz ki $z_1,z_2,…,z_H$’nin tanımladığı $H$ boyutlu uzayda doğrusal model kullanılabilsin.
Bunu bir kerede yapamazsak bu taban modellerini ardışık da tanımlayabiliriz. Yani birinci “katman”da girdiyi kullanırken
$$z_i^{(1)}=g(x_1, x_2|v_i^{(1)}),~~~~~~ i=1,…, H_1$$
ikinci katmanda, birinci katmanın çıktısını girdi olarak kullanabiliriz:
$$z_j^{(2)}=g(z_1^{(1)}, …, z_{H_1}^{(1)}|v_j^{(2)}),~~~~~~ j=1, … H_2~~~~~~~~~(3)$$
Ve ardından çıktıyı ikinci katman çıktılarının doğrusal birleşimi olarak yazarız:
$$y=w_0 +w_1 z_1^{(2)} +w_2 z_2^{(2)}+…+w_{H_2} z_{H_2}^{(2)}$$
Bu şekilde devam edip istersek ikiden fazla katman da tanımlayabilirdik. Amacımız en son $z$ katmanında çıktının doğrusal olmasını sağlamak.
Böyle tanımladığımız model oldukça esnek ama bu yaklaşımın en büyük sorunu şu: Doğrusal modelin aksine bu modelde veri üstündeki hatayı en düşük yapacak parametre değerlerini (burada tüm $v$ ve $w$ değerleri) bulmak için bir yöntemimiz yok; kullandığımız yöntemlerin hiçbiri en iyi çözümü bulmayı garanti etmiyor.
Yapay Sinir Ağları
Peki nöron bunun neresinde, ve tüm bunların sinir ağlarıyla ne ilgisi var, diye sorabilirsiniz.
Yapay sinir hücresi girdilerin ağırlıklı toplamı olarak yazılır. Denklem (1) aynı zamanda algılayıcı denilen yapay sinir ağı modelini tanımlıyor. Yukarıda kullandığımız taban fonksiyonu da özyinelemeli bir biçimde yine bir algılayıcı olabilir:
$$g(x_1, x_2|v_0, v_1, v_2)=f(v_0+v_1 x_1 +v_2 x_2)$$
Burada $f$ olarak gösterilen etkilenim fonksiyonudur ve doğrusal olmayan dönüşümü sağlar. $f$ genelde bir tür eşik fonksiyonudur: $f(a), a>0$ ise 1 (ya da $a$), değilse 0 değerini alır. Ve bunun sonucu olarak girdi uzayının bir kısmında değeri sıfır iken kalanında sıfırdan farklıdır, yani taban fonksiyonu orada çıktıya etki eder.
Yukarıdaki $g(x_1, x_2|v_0, v_1, v_2)$ taban fonksiyonun sıfır olmayan bir değer alması için gereken koşul
$$v_0+v_1 x_1+v_2 x_2 > 0$$
ya da
$$v_1 x_1 +v_2 x_2 >-v_0$$
ya da
$${\bf v}^T {\bf x} > -v_0$$
Burada ${\bf x}$ ile gösterilen bütün girdilerden oluşan vektör (burada iki boyutlu), ${\bf v}$ ile gösterilen de tüm ağırlıklar (burada iki boyutlu). İç çarpım iki vektörün benzerliğini ölçüyor, dolayısıyla ${\bf x}$ ile ${\bf v}$ arasındaki benzerlik eğer $-v_0$ eşik değerinden küçük olursa $g$ sıfır değerini alıyor, ve toplam çıktıya katılmıyor; ama eğer benzerlik yeterince büyükse $g$ sıfırdan büyük bir değer alıyor ve o taban fonksiyonu çıktıya katkı yapıyor. Yani her taban fonksiyonu kendi ${\bf v}$ vektöründe bir şablon taşıyor ve girdinin o şablona ne kadar benzediğine göre $g$ sıfır ya da sıfırdan büyük bir değer alıyor.
Yukarıda tanımladığımız denklem (2)’yi çok katmanlı bir sinir ağı olarak düşünebiliriz. Taban fonksiyonlarının çıktısı olan $z_1, …, z_H$ sinir ağının saklı birimleridir ve girdi katmanı ($x$ değerleri) ile çıktı katmanı ($y$ değeri) arasında bir saklı katman tanımlar. Taban fonksiyonlarının şablonları olan ${\bf v}$ vektörleri de bu saklı birimlere gelen ağırlıklara karşılık geliyor. Öğrenme sırasında hem o şablonları, hem de $v_0$ benzerlik eşiklerini veriden öğreniyoruz.
Denklem (2)’de bir tane saklı katman var, denklem (3) ise iki saklı katmanlı bir yapay sinir ağına karşılık geliyor: $z^{(1)}$ girdinin ağırlıklı toplamıyla hesaplanan birinci saklı katmanı, $z^{(2)}$ ise birinci saklı katmanın ağırlıklı toplamıyla hesaplanan ikinci saklı katmanı tanımlıyor. Saklı katman sayısı çok olunca buna derin sinir ağı, böyle bir ağın ağırlıklarını (tüm saklı katmanlardaki $v$ değerleri ve en son saklı katmandan çıktıya giden $w$ değerleri) verideki hatayı en aza indirecek biçimde hesaplamaya derin öğrenme diyoruz.
Derin sinir ağı eğitiminde farklı sorunlar var. Öncelikle öğrenme kümesinde en küçük hatayı bulmamızı garanti eden bir yöntemimiz olmadığını yukarıda söyledik. En sık kullanılan hata geri yayma yöntemi, eğim inişi kullanıyor ve bu, başlangıç noktasına en yakın yerel en iyi çözüme yakınsıyor. Yakınsama hızını arttırmak için bazı teknikler olsa da bulduğumuz çözümün kalitesi konusunda bir şey söyleyemiyoruz.
İkinci bir sorun, sinir ağının yapısını, yani saklı katman sayısı ve katmanlardaki saklı birim sayısını ayarlamak için deneme-yanılmadan başka yöntemimiz yok. Farklı uygulamalarda iyi çalıştığı bilinen yapılar var, bunları uygun oldukları durumda kullanıyoruz; ama bunların da her zaman ne kadar iyi çalışacağını bilmiyoruz.
Ağ yapısını tanımlarken en faydalı yaklaşımlardan biri evrişim katmanları. Buradaki amaç girdideki yapıyı ağın yapısına yansıtmak. Örneğin bir görüntünün iki boyutlu (resmin eni ve boyu) olduğunu biliyoruz, her piksel ona bu iki boyutta en yakın komşu piksellerle ilintili (çünkü çoğu zaman aynı nesnenin parçalarına karşılık geliyorlar) ama çok uzaktaki piksellerle ilintili değil, demek ki piksellere bakarken çok uzak olanlara birlikte bakmaya gerek yok. Evrişim katmanlarındaki saklı birimlerin girdisi dolayısıyla bir önceki katmandaki tüm değerler değil, girdideki küçük bir alan, ve o alanda küçük bir şablona bakılıyor. Yani evrişim dediğimiz esasında girdisi belli bir yerel alana kısıtlanmış bir tür taban fonksiyonu.
Evrişim katmanlarını art arda koyarak girdide gittikçe daha büyük alanlarda ve gittikçe daha soyut öznitelikleri öğrenebiliyoruz. Örneğin büyük bir resimde ilk evrişim katmanları kısa çizgileri tanımayı öğrenirken (ağırlık şablonları o tür çizgilere en fazla tepkiyi verecek biçimde), sonraki katman onları birleştirip daha uzun çizgileri ya da köşeleri öğreniyor, sonraki katman çemberleri, dikdörtgenleri tanıyor, vs. Her katmanda girdideki her noktaya uygulanan birden çok evrişim şablonu var ve bunların çıktılarına öznitelik haritası diyoruz. Bir öznitelik haritasında yan yana pikseller için hesaplanan şablon çıktıları birbirine çok benzeyeceğinden boyut sayısını ve dolayısıyla karmaşıklığı azaltmak için yan yana birkaç pikselden yalnızca birini üst katmana geçiriyoruz, buna altörnekleme deniyor.
Evrişim de eski bir yöntem, sinyal işlemede yıllarca farklı uygulamalar için önerilmiş evrişim şablonları var, ama bu şablonların en sonda istenen çıktıya göre öğrenilmesi yeni. Uçtan uca öğrenme denilen şey bu: İlk katmanlardaki ağırlıkların bile en sondaki çıktıdaki hatayı en aza indirecek biçimde ayarlanması.
Derin Öğrenme Örnekleri
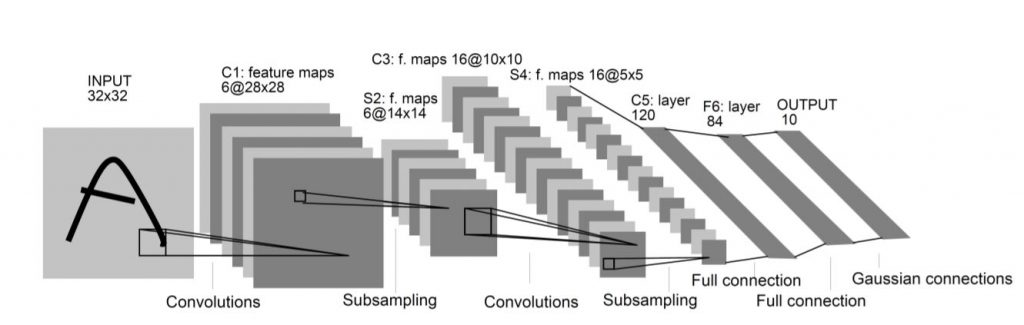
Bu bağlamda en iyi örnek, bu yıl Turing ödülü alanlardan Yann Le Cun tarafından tasarlanan ve derin öğrenme düşüncesini başlatan LeNet-5 ağı [1]:
Derin ağların yeniden ortaya çıkması 2012’de AlexNet’le [2] oldu ve o zamandan beri ilgi azalmadan sürüyor. Bu yıl Turing ödülünü alanlardan Geoffrey Hinton, AlexNet’i tasarlayan Alex Krizhevsky’nin tez hocası; aynı zamanda hata geri yayma algoritmasının anlatıldığı 1986 tarihli makalenin [3] yazarlarından da biri. Başkalarının yüz çevirmesine rağmen sinir ağları konusundaki araştırmalarını hep devam ettirmiş.
AlexNet yine görüntü tanıma üstüne ama LeNet-5 gibi 10 tane değil 1.000 tane sınıf tanıyor; girdi görüntüsü de daha büyük, 32×32 yerine 256×256. 11 katmanı ve toplam 60 milyon parametresi var, öğrenme verisi de (ImageNet) çok daha büyük, 1.2 milyon görüntü içeriyor. Ve bir başka yenilik ağın çalışmasının grafik işlem birimi üstünde hızlandırılmış olması. 2012’de AlexNet’in bu veri üstünde o ana dek erişilebilenlerden çok daha düşük tanıma hatasına inebilmesi yapay öğrenme ve örüntü tanıma üstünde çalışan herkese, daha büyük veri üstünde eğitilen daha büyük (derin) ağlarla daha zor problemlerin çözülebildiğini gösterdi.
AlexNet’ten bu yana derin ağlar çok farklı uygulamalarda başarıyla kullanılıyor. Bunlar arasında görüntü tanımadan sonra üzerinde en çok çalışılan konu doğal dil işleme. Burada Turing ödülünü alan üçüncü kişi Yoshua Bengio’nun öne çıkan çalışmaları [4] var. Yukarıda yapay sinir ağının saklı katmanlarından ve bu saklı katmanlarda art arda gittikçe soyut biçimde farklı şablonların tanındığından bahsettik. İşte herhangi bir girdi için bu saklı katmanlardaki $z$ değerleri girdinin soyut bir gösterimini oluşturuyor; burada birçok $z$ değeri sıfırdan farklı olduğu için buna dağıtık gösterim deniyor ve ağdaki tüm ağırlıklar veriden öğrenildiği için uygulamaya en iyi uyan gösterim oluyor. Derin öğrenmeyi zaten ilginç yapan en önemli yanlardan biri de bu, yani veriden bu tür gösterimlerin, farklı katmanlarda farklı soyutluk düzeylerinde öğrenilebilmesi. Örneğin doğal dil işlemede bu biçimde sözcükler için öğrenilen dağıtık gösterimler sözcükler arasındaki sözdizimsel ya da anlamsal ilişkileri yansıtabiliyor.
Sonuç
Derin öğrenmenin birçok uygulamada çok başarılı sonuçlar verdiğini biliyoruz. Görüntü tanıma, bir dilde ötekine çeviri, konuşma tanıma gibi farklı uygulamalarda şu anda en iyi çalışan yaklaşımlar derin öğrenmeye dayanıyor. Esasında bu son on yılda kuramsal olarak fazla bir katkı yapılmadı, bugün kullanılan öğrenme yöntemleri 1990’ların başlarında da biliniyordu. Yapay sinir ağlarının derin öğrenme dediğimiz bu ikinci dalgasındaki yenilik, yukarıda da bahsettiğim gibi, daha çok veri ve daha çok hesap sayesinde. Günümüzde akıllı telefonlar ve başka akıllı sayısal cihazlar sayesinde çok daha fazla verimiz var, ve çok çekirdekli işlemciler ve grafik işlem birimleri sayesinde hesaplama gücümüz de çok daha arttı. Dolayısıyla daha büyük ağları daha büyük veriyle eğiterek birçok uygulamada başarıyı arttırmayı başardık. Bu iki kaynak, yani veri ve hesaplama gücü arttıkça başarı da artacaktır. Son yıllarda bu çalışmaların ticarileşebilecek ürün düzeyine ulaşmış olması da ek bir itici güç; araştırma ve geliştirmeye çok daha fazla kaynak aktarılabilmesini sağlıyor.
Bütün bu araştırmalar ve gittikçe daha çok veriyle eğitilen gittikçe daha büyük ağlar bir gün bizi insan düzeyinde zekâya ulaştıracak mı, onu zaman gösterecek.
Ethem Alpaydın
Bilim Akademisi üyesi
Boğaziçi Üniversitesi Bilgisayar Mühendisliği Bölümü emekli öğretim üyesi
Kaynaklar
[1] LeCun, Y., Bottou, L., Bengio, Y., Haffner, P. (1998). “Gradient-based learning applied to document recognition.” Proceedings of the IEEE, 86: 2278–2324.
[2] Krizhevsky, A., Sustkever, I., Hinton, G.E. (2012). “ImageNet Classification with Deep Convolutional Neural Networks.” Advances in Neural Information Processing Systems 25, 1097–1105.
[3] Rumelhart, D. E., Hinton, G. E., Williams, R. J. (1986). “Learning Representations by Back-propagating Errors.” Nature, 323: 533–536.
[4] Bengio, Y., Ducharme, R., Vincent, P. (2003). “A Neural Probabilistic Language Model.” Journal of Machine Learning Research, 3: 1137–1155.