Sözlük tanımları, çoğu zaman bir çerçeve çizmek ve yön vermek açısından yararlıdır. Bu nedenle isterseniz biz de bir sözlük tanımı ile başlayalım:
Bilgi Kuramı (enformasyon teorisi), iletişim probleminin modellenmesi ve çözümlenmesi (analizi) ile ilgilenen mühendislik bilimi ve matematik alanıdır.
Peki iletişim problemi nedir?
Claude Elwood Shannon, Bilgi Kuramı alanını kuran çalışma olarak kabul edilen makalesinde[1]Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27 (3), 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, iletişim problemini şöyle tanımlar:
“Belirli bir noktada seçilen bir iletinin (mesajın) başka bir noktada kesin ya da yaklaşık olarak yeniden elde edilmesi”[2]“The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.”
Aynı makalede Shannon, iletişim problemini Şekil 1’de verilen şema üzerinden açıklar.
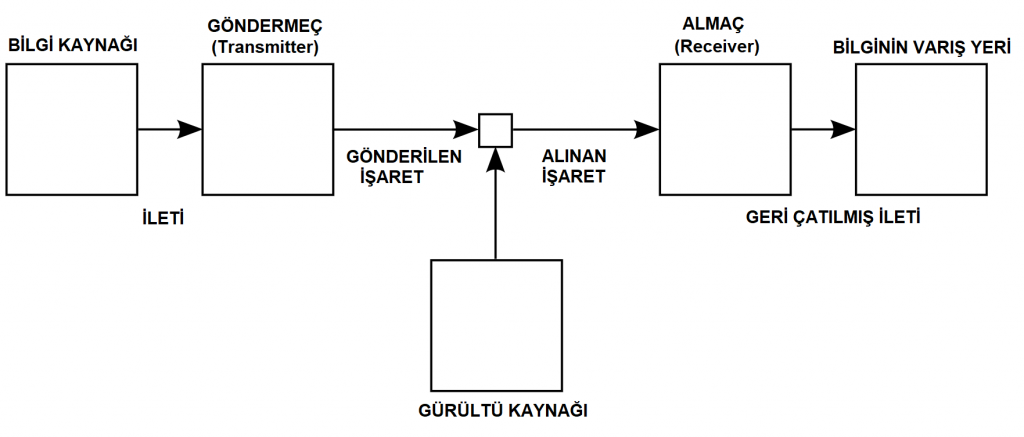
Sekil 1’de göndermeç ve almaç iletişimi sağlamak için yapılan tasarımı, bilgi kaynağı ve gürültü kaynağı ise iletişim problemini tanımlayan dışsal etkenleri temsil eder. İletişim sistemi her kullanıldığında ilkin, bilgi kaynağı gönderilecek iletiyi seçer. Sonra göndermeç bu iletiye karşılık gelen işaretler serisini gönderir. İletişim kanalı, gürültü kaynağının etkisi ile gönderilen işaretler serisini alınan işaretler serisine dönüştürür. Almaç da alınan işaretler serisini kullanarak geri çatılmış (yeniden elde edilmiş) iletiyi belirler. Göndermecin hangi ileti için hangi işaret serisini kullanacağına dair kurallar kodlamayı; almacın hangi alınan işaret serisi için hangi geri çatılmış iletiyi seçeceğine dair kurallar da kod çözümünü oluşturur.
Hem göndermecin kullandığı kodlama, hem de almacın kullandığı kod çözümü iletişim sistemi kullanılmadan önce belirlenir. Bu aşamada, göndermeç ve almaç tasarlanırken, bilgi kaynağının hangi iletiyi seçeceği bilinmese de her bir iletinin seçilmesinin ne kadar olası olduğu bilinir. Bir başka deyişle bilgi kaynağının istatistiksel davranışı bilinmektedir. Aynı şekilde göndermeç ve almaç tasarlanırken gönderilen bir işaret serisinin iletişim kanalı tarafından hangi alınan işaret serisine dönüştürüleceği mutlak olarak bilinmese de, iletişim kanalının istatistiksel davranışı bilinir.
Bir örnek: Deniz feneri ve mors alfabesi yardımıyla iletilen metin
Hem bilgi kaynağı ve iletişim kanalı kavramlarını, hem de bir mühendislik ve matematik problemi olarak iletişim problemini daha somut ve anlaşılır yapmak için örnek bir iletişim problemine daha yakından bakalım. Bir metnin, bir deniz fenerinin ışığı ve Mors alfabesi kullanılarak iletilmesi problemini ele alalım.
Bu problemde ileti metindir. Metni iletecek olanlar ne metnin seçimi üzerinde bir kontrole sahiptirler, ne de hangi metnin seçileceğini bilirler. Metni iletecek olanlar hangi metnin seçildiğini öğrenmeden önce metindeki her bir karakterin kısa ve uzun çizgiler cinsinden nasıl ifade edileceği konusunda, yani hangi Mors alfabesini kullanacakları konusunda, anlaşırlar. Metin onu iletecek olanlar tarafından öğrenildiğinde seçilmiş olan Mors alfabesi yardımıyla kısa ve uzun çizgiler, karakterler arası boşluklar ve kelimeler arası boşluklar türünden ifade edilir.
Metnin bu yeni alfabedeki ifadesini iletmek için deniz fenerinin ışığı çeşitli şekillerde kullanılabilir. Bu kuralların ne olacağının da, tıpkı çeşitli karakterlerin yeni alfabede nasıl temsil edileceğine dair kurallar gibi, önceden belirlenmesi gerekir. Örneğin ışık kısa çizgileri ifade etmek için bir saniye, uzun çizgileri ifade etmek için ise üç saniye boyunca açık tutulabilir. Benzer şekilde ışık metindeki karakterleri ifade etmek için kullanılan çizgiler arasında bir saniye, her bir karaktere dair çizgilerin tümü bittikten sonra iki saniye, ve her bir kelimeye ait çizgilerin tümü bittikten sonra beş saniye süreyle kapalı tutulabilir.
Deniz fenerini kullananlar ışığın açılıp kapanmasını istedikleri gibi kontrol edebilseler bile, deniz fenerini uzaktan izleyip metni yeniden oluşturacak olanların deniz fenerinin ışığının hangi anda açılıp hangi anda kapandığını hatasız bir şekilde izlemeleri her zaman mümkün olmayabilir. Örneğin bir fırtına sırasında yağış veya dalgalar, deniz fenerinin ışığı açık olduğu halde kapalı gibi görünmesine veya başka bir ışık kaynağı, deniz fenerinin ışığı kapalı olduğu halde açık gibi görünmesine neden olabilir. Tüm bu etkilere rağmen çoğu kez metin önce seçilmiş olan Mors alfabesinde — bazı hatalarla bile olsa — sonra da ilkin yazıldığı alfabede yeniden elde edilebilir.
Bu örnekte hangi metnin iletileceğinin seçimi bilgi kaynağını, deniz fenerinin ışığının açılıp kapanması ve bunun uzaktan gözlemlenmesi ise iletişim kanalını temsil ediyor. İletişim sistemleri tasarlanırken bilgi kaynağının ve iletişim kanalının istatiksel davranışı hakkında kabuller yapılır. Bu örnekte bilgi kaynağı ile ilgili metnin hangi alfabede yazılacağına dair bir kabul vardır; örneğin yukarıda bahsedilen kurallar Latin alfabesi için uygulandığından Latin alfabesi ile yazılmış herhangi bir metin iletilebilir. İletişim kanalı ile ilgili ise deniz feneri ile onu izleyenler arasına giren bir cismin ne sıklıkla deniz fenerinden gelen ışığı engelleyebileceğine ve ışık kirliliği ile yansımaların deniz fenerinin ışığının kapalı olması durumunda bile açık olduğu izlenimini ne sıklıkla yaratabileceğine dair kabuller vardır.
Bilgi kaynağı ve iletişim kanalının önceden mutlak olarak bilinemeyecek bu davranışlarına rağmen iletinin başarılı bir şekilde yeniden elde edilebilmesi için göndermeçte yapılanlara kodlama, almaçta yapılanlara da kod çözümü ismini verdiğimizi hatırlayalım. Bu örnekte deniz fenerinin ışığının açılıp kapanmasını metne bağlı olarak belirleyen kuralların tümü kodlamayı oluşturur; kod çözümü ise deniz fenerinin gözlenen davranışını kullanarak metni yeniden elde etmek için kullanılan kuralların tümünden oluşur.
Bir kodun başarımının ölçütleri nelerdir?
Kodlama ve kod çözümünden oluşan kurallar bütünü kısaca kod olarak da isimlendirilir. Bir kodun başarımının (performansının) iki temel ölçütü vardır: kodun simge iletim hızı ve kodun hata olasılığı. Kodun simge iletim hızı birim zamanda iletilen kaynak simgesi[4]Tartıştığımız örnekte kaynak simgeleri metni oluşturan satırlar veya karakter/harfler olarak düşünülebilir. sayısıdır. Kodun hata olasılığı ise kaynağın sağladığı iletinin başarılı bir şekilde iletilememesi olasılığıdır. Yüksek başarımlı bir sistemde mümkün olduğu kadar yüksek simge iletim hızı ve mümkün olduğu kadar düşük hata olasılığı hedeflenir. Ele aldığımız örnekte kodun simge iletim hızı kodun bir dakikada gönderdiği ortalama satır sayısı, veya karakter/harf sayısı, olarak düşünülebilir. Tabii böyle bir ortalamayı hesaplamak için hangi metnin ne olasılık ile seçildiğini bilmemiz de gerekir. Benzer şekilde kodun hata olasılığı metnin hatasız bir şekilde yeniden elde edilememesi olasılığıdır. Bu olasılığı hesaplamak için hangi metnin ne olasılıkla seçileceği bilgisinin yanı sıra kanalın davranışı hakkında yukarıda değindiğimiz bilgilere sahip olmamız gerekir.
Shannon’un müjdesi: Simge iletim hızını düşürmeden hata olasılığını düşürmek mümkün
Birçok iletişim probleminde kodun hata olasılığının olabildiğince küçük olması gereklidir. İlk bakışta bunun ancak simge iletim hızını düşürerek sağlanabileceği düşünülebilir. Fakat Shannon’un makalesinde[5]Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27 (3), 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x gösterdiği üzere bu izlenim doğru değil. Çoğu iletişim problemince sağlanan birtakım genel kabuller geçerli olduğu sürece belirli bir sınırın altındaki tüm simge iletim hızlarında seçebileceğimiz her pozitif sayıdan daha küçük bir hata olasılığına sahip bir kod vardır ve bu sınırın üzerindeki her simge iletim hızında kodların hata olasılığı simge iletim hızının değerine de bağlı olan bir pozitif sayıdan daha küçük olamaz.
Peki ilgilendiğimiz herhangi bir iletişim problemi için bu sınır nedir, nasıl belirlenir? İsterseniz bu soruları yine örneğimiz üzerinden cevaplamaya çalışalım. Örneğimizde metin, yani ileti, önce kısa ve uzun çizgilerden, karakterler arası boşluklardan, ve kelimeler arası boşluklardan oluşan dört harfli bir alfabede ifade edilmişti. Bu dört harfli alfabenin harflerinin her birini iki basamaklı (haneli) ikili (binary) bir sayı olarak ifade edebiliriz. Örneğin kısa çizgiler “10” sayısıyla, uzun çizgiler “11” sayısıyla, karakterler arası boşluklar “01” sayısıyla ve kelimeler arası boşluklar “00” sayısıyla ifade edilebilir. Böyle bir ornatma (yerine koyma işlemi) kullanarak metnin dört harfli alfabedeki ifadesinden metnin ikili (binary) bir sayı olarak ifadesini ve aynı ornatmanın tersini kullanarak metnin ikili bir sayı olarak ifadesinden metnin dört harfli alfabedeki ifadesini elde edebiliriz. Dolayısıyla kodlama ve kod çözümü sırasında metnin dört harfli alfabedeki ifadesi yerine metnin ikili bir sayı olarak ifadesinin elde edildiğini düşünebiliriz.

- Metnin ikili bir sayı olarak ifade edilmesi için uygulanan kurallar kaynak kodlaması, bu ikili sayıdan metnin elde edilmesi için uygulanan kurallar ise kaynak kod çözümü olarak adlandırılır. Örnekte bahsettiğimiz kaynak kodunun bir satırını ifade etmek için ihtiyaç duyacağı ikili sayının basamak (hane) sayısının ortalaması bu kaynağın bir satırının bit (binary digit) sayısıdır. Tüm olası kaynak kodları arasında, en verimli olanının (en az bite ihtiyaç duyanının) metnin bir satırı için ihtiyaç duyacağı bit sayısı kaynağın bir satırının ortalama entropisine eşittir.[6]Daha doğru bir ifade ile kaynağın entropisinin satır sayısına bölümüne eşit olacaktır. Ama bu yazıdaki amaçlarımız için bu iki büyüklüğün eşit olduğu kabul edilebilir.[7]Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27 (3), 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x
- Benzer şekilde deniz fenerinin ışığını kullanarak metne karşılık gelen ikili sayıyı, deniz fenerinin ışığını gözleyenlere iletmek için kullanılan kuralların tümü kanal kodunu oluşturur. Metne karşılık gelen ikili sayıya, bağlı olarak deniz fenerinin ışığının nasıl açılıp kapanacağını belirleyen kuralların tümüne kanal kodlaması, fenerin gözlenen davranışını kullanarak metne karşılık gelen ikili sayıyı elde etmek için kullanılan kuralların tümüne kanal kod çözümü denir. Bir kanal kodunun bilgi iletim hızı birim zamanda ilettiği bit sayısına (birim zamanda ilettiği ikili sayı basamağı sayısına) eşittir. Bir bilgi iletim hızı ancak seçebileceğimiz her pozitif sayı için ondan daha küçük bir hata olasılığına sahip ve bu bilgi iletim hızında bir kod varsa erişilebilir olarak tanımlanır. Bir iletişim kanalındaki en yüksek erişilebilir bilgi iletim hızı o kanalın kapasitesidir. Sonuç olarak hata olasılığını istediğimiz kadar düşürebilmek için birim zamanda gönderdiğimiz bit sayısının kanal kapasitesinden düşük olması gerekir.[8]Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27 (3), 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x
Temel sınırlar: Entropi ve kanal kapasitesi
Elimizde bir satırının ortalama entropisi H bit olan bir bilgi kaynağı ve kapasitesi saniyede C bit olan bir iletişim kanalı olduğunda, kodlama için önce kaynak kodlaması daha sonra da kanal kodlaması uygulayarak, kod çözümü için ise önce kanal kod çözümü daha sonra da kaynak kod çözümü uygulayarak hata olasılığı istediğimiz kadar küçük olan bir kod bulmamız mümkündür. Bulduğumuz kod tasarımı gereği saniyede C/H satır iletecektir. Buna ek olarak saniyede C/H’den daha fazla satır gönderen tüm kodların hata olasılığının pozitif bir sayıdan büyük olması gerektiğini gösterebiliriz. Dolayısıyla daha önce bahsettiğimiz simge iletim hız sınırı iste bu C/H değeridir.
İletinin düşük hata olasılıklarında iletilmesinin imkânlı olduğu hızların sınırı sadece yukarıda tartıştığımız örnekte değil, birtakım genel kabulleri sağlayan tüm iletişim problemlerinde, kaynağın bir sembolünün ortalama entropisi H ve kanal kapasitesi C cinsinden C/H olarak ifade edilebilir. Aynı zamanda bu iletişim problemlerinin hepsinde, bu sınırın altındaki her hıza ve istenilen her hata olasılığına bir kaynak kodu ile bir kanal kodunu yukarıdaki örnekte tarif edildiği şekilde birlikte kullanarak erişen bir kod vardır.
Kimi durumlarda —örneğin ses veya görüntü işaretlerinin iletilmesi problemlerinde olduğu üzere olası iletilerin kümesi sayılamaz (uncountable) olduğunda— iletişim kanalı çıktısında bilgi kaynağının iletisine yeterince yakın bir iletinin yeniden elde edilmesi iletinin başarıyla iletilmesi olarak tanımlanır. Örneğin bir telefon görüşmesinde yeniden üretilen (geri çatılan) sesle kaynaktaki sesin mutlak olarak aynı olması gerekli değildir, ona yeterince yakın olması yeterlidir. Böyle problemlerde de iletinin başarıyla iletilebileceği en yüksek hızın belirlenmesi için bilgi kaynağının ve iletişim kanalının ayrı ayrı incelenmesi yeterlidir ve bu sınırın altındaki her hıza bir kaynak kodu ile bir kanal kodunun birlikte kullanılmasından oluşan kodlar ile erişilebilir.
Bu gözlemler, iletişim sisteminin tümü için bir kod tasarlamak yerine bilgi kaynağı için bir kaynak kodunu ve iletişim kanalı için bir kanal kodunu birbirinden bağımsız olarak tasarlayıp birlikte kullanmanın, en azından iletişim sistemlerinin erişebileceği hızlar açısından, bir performans kaybına sebep olmayacağına işaret ediyor. İnternetten, mobil uygulamalara, dijital yayınlardan, telekonferans sistemlerine hayatımızın bir parçası olan iletişim sistemlerinin hepsinde kullanılan sayısal iletişim mimarisi bu gözlemden de esinlenerek yapılmış son derece başarılı bir tasarım varsayımıdır/tercihidir.
Barış Nakiboğlu[9]Yazar Bülent Sankur’a teknik terimlerin kullanımı ile ilgili öneri ve eleştirileri için, Güneş Nakiboğlu, Bülent Sankur ve Defne Üçer Şaylan’a yazının daha anlaşılır ve akıcı olması için yaptıkları öneriler için teşekkür eder.
ODTÜ Elektrik ve Elektronik Mühendisliği Bölümü (BAGEP 2019)
 Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Bu eser Creative Commons Atıf-GayriTicari 4.0 Uluslararası Lisansı ile lisanslanmıştır. İçerik kullanım koşulları için tıklayınız.
Notlar/Kaynaklar
| ↑1, ↑3, ↑5, ↑7, ↑8 | Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27 (3), 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x |
|---|---|
| ↑2 | “The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.” |
| ↑4 | Tartıştığımız örnekte kaynak simgeleri metni oluşturan satırlar veya karakter/harfler olarak düşünülebilir. |
| ↑6 | Daha doğru bir ifade ile kaynağın entropisinin satır sayısına bölümüne eşit olacaktır. Ama bu yazıdaki amaçlarımız için bu iki büyüklüğün eşit olduğu kabul edilebilir. |
| ↑9 | Yazar Bülent Sankur’a teknik terimlerin kullanımı ile ilgili öneri ve eleştirileri için, Güneş Nakiboğlu, Bülent Sankur ve Defne Üçer Şaylan’a yazının daha anlaşılır ve akıcı olması için yaptıkları öneriler için teşekkür eder. |






